题目内容
设x、y∈R，在直角坐标平面内，| ? |
| a |
| ? |
| b |
| ? |
| a |
| ? |
| b |
分析：利用向量的模将：“|
|+|
|=8，”用点M的坐标表示出来，再结合式子的几何意义，根据椭圆的定义即可求得答案．
| ? |
| a |
| ? |
| b |
解答：解：∵|
|+|
|=8，
∴
+
=8，
此式的几何意义是：
动点（x，y）到两个定点（0，-2）、（0，2）的距离之和等于8，
由椭圆的定义知：点M（x，y）的轨迹方程为椭圆．
其长轴长为8，焦距为4．焦点在y轴上．
其方程为：
+
=1．
故答案为：
+
=1．
| ? |
| a |
| ? |
| b |
∴
| x2+(y+2)2 |
| x2+(y-2)2 |
此式的几何意义是：
动点（x，y）到两个定点（0，-2）、（0，2）的距离之和等于8，
由椭圆的定义知：点M（x，y）的轨迹方程为椭圆．
其长轴长为8，焦距为4．焦点在y轴上．
其方程为：
| x2 |
| 12 |
| y2 |
| 16 |
故答案为：
| x2 |
| 12 |
| y2 |
| 16 |
点评：本题利用定义法求轨迹方程．定义法：若动点轨迹的条件符合某一基本轨迹的定义（如椭圆、双曲线、抛物线、圆等），可用定义直接探求
练习册系列答案
相关题目
，
为直角坐标系平面内x轴、y轴正方向上的单位向量，若向量
＝x
)
＝x
)
的直线l与轨迹C交于不同两点A、B，求△PAB面积的最大值．
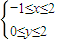所表示的平面区域是W，从区域W中随机取点M（x，y）．