题目内容
【题目】已知![]() ,
,![]() 是椭圆
是椭圆![]() 的左右焦点,椭圆与
的左右焦点,椭圆与![]() 轴正半轴交于点
轴正半轴交于点![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,且
,且![]() 到直线
到直线![]() 的距离为
的距离为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)![]() 为椭圆
为椭圆![]() 上任意一点,过
上任意一点,过![]() ,
,![]() 分别作直线
分别作直线![]() ,
,![]() ,且
,且![]() 与
与![]() 相交于
相交于![]() 轴上方一点
轴上方一点![]() ,当
,当![]() 时,求
时,求![]() ,
,![]() 两点间距离的最大值.
两点间距离的最大值.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)设出![]() 的方程,根据其斜率以及点到直线的距离,即可列出方程,求得结果;
的方程,根据其斜率以及点到直线的距离,即可列出方程,求得结果;
(2)根据题意,得到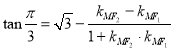 ,从而求得
,从而求得![]() 点的轨迹方程,将问题转化为求一点到圆上任意一点距离的最大值,则问题得解.
点的轨迹方程,将问题转化为求一点到圆上任意一点距离的最大值,则问题得解.
解:(1)由题意,可知![]() ,
,![]() ,
,![]() .
.
∴![]() ①.
①.
∵直线![]() 的方程为
的方程为![]() ,即
,即![]() .
.
∴由题意有![]() ②.
②.
又![]() ③.
③.
由①②③得![]() ,
,![]() ,
,![]() .
.
∴椭圆![]() 的方程为
的方程为![]() .
.
(2)由(1)可知:![]() ,
,![]() .
.
设![]() ,
,![]() 且
且![]() .
.
则当![]() ,
,![]() 都不垂直于
都不垂直于![]() 轴时,
轴时,![]() ,
,![]() .
.
∵![]() ,
,
∴![]() .
.
∴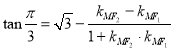 .
.
化简,得![]() .
.
当![]() 或
或![]() 垂直于
垂直于![]() 轴时,得
轴时,得![]() ,也满足上式.
,也满足上式.
∴![]() 点的轨迹方程为
点的轨迹方程为![]() .
.
∴当![]() 与圆心
与圆心![]() 距离最大时,
距离最大时,![]() ,
,![]() 两点间距离取得最大值.
两点间距离取得最大值.
∵![]()
![]()
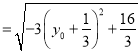 .
.
又∵![]() ,
,
∴![]() .
.
∴![]() ,
,![]() 两点间距离的最大值为
两点间距离的最大值为![]() .
.

练习册系列答案
相关题目