题目内容
方程x2+y2-2ax+2ay=0所表示的圆( )
分析:根据圆的标准方程的特征,求出圆心和半径,根据圆心(a,-a)在直线x+y=0上,从而得出结论.
解答:解:方程x2+y2-2ax+2ay=0 即 (x-a)2+(y+a)2=2a2,表示以(a,-a)为圆心,半径等于
|a|的圆.
由于圆心(a,-a)在直线x+y=0上,故方程x2+y2-2ax+2ay=0所表示的圆关于直线x+y=0对称,
故选C.
| 2 |
由于圆心(a,-a)在直线x+y=0上,故方程x2+y2-2ax+2ay=0所表示的圆关于直线x+y=0对称,
故选C.
点评:本题主要考查圆的标准方程的特征,判断圆心(a,-a)在直线x+y=0上,是解题的关键,属于中档题.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案
相关题目
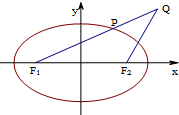 已知椭圆
已知椭圆