题目内容
若
且
，则
的最小值是（ ）
A． | B．1 | C．4 | D．8 |
C
解析试题分析：
又因为，所以
，当且仅当
时取等号.
考点：本小题主要考查基本不等式和“1”的整体代换的应用.
点评：应用基本不等式求最值要注意“一正二定三相等”三个条件缺一不可.
练习册系列答案
阅读快车系列答案
相关题目
函数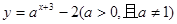
的图像恒过定点A，且点A在直线
上
，则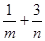
的最小值为（ ）
| A．12 | B．10 | C．8 | D．14 |
已知
，由不等式
……
可以推出结论
=
| A．2n | B．3n | C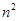． | D． |
若正数
满足
，则
的最小值是（ ）
A． | B． | C． | D． |
若
且满足
，则
的最小值是（ ）
A． | B． | C． | D． |
若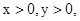
且
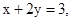则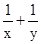
的最小值为（ ）
A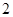． | B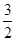． | C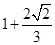． | D． |
若
，则
的最小值是（ ）
A． | B． | C．2 | D．3 |
设正实数
满足
，则当
取得最大值时，
的最大值为( )
A． | B． | C． | D． |
且
则此四个数
中最大的是（ ）
Ｂ 
Ｃ 
Ｄ 