题目内容
20.函数y=[x]叫做“取整函数”,其中符号[x]表示x的整数部分,即[x]是不超过x的最大整数,例如[2]=2;[2.1]=2;[-2.2]=-3,那么[lg1]+[lg2]+[lg3]+…+[lg2016]的值为4941.分析 分类讨论,当1≤n≤9时,[lgn]=0;当10≤n≤99时,[lgn]=1;当100≤n≤999时,[lgn]=2;当1000≤n≤9999时,[lgn]=3;从而分别求和即可.
解答 解:当1≤n≤9时,
[lgn]=0,
当10≤n≤99时,
[lgn]=1,
当100≤n≤999时,
[lgn]=2,
当1000≤n≤9999时,
[lgn]=3,
故[lg1]+[lg2]+[lg3]+…+[lg2016]
=0×9+1×90+2×900+3×1017
=90+1800+3051
=4941,
故答案为:4941.
点评 本题考查了分类讨论的思想应用及对数运算的应用.

练习册系列答案
相关题目
15.设函数f(x)=cos2x-2sinxcosx-sin2x,g(x)=2cos2x+2sinxcosx-1,把f(x)的图象向右平移m个单位后,图象恰好为函数g(x)的图象,则m的值可以是( )
| A. | π | B. | $\frac{3π}{4}$ | C. | $\frac{π}{2}$ | D. | $\frac{π}{4}$ |
 在边长为1的正方体ABCD-A1B1C1D1中.
在边长为1的正方体ABCD-A1B1C1D1中.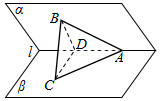 如图所示,二面角α-l-β的面α内有一条直线AB,它与棱l的夹角为45°.AB与平面β所成的角为30°.求这个二面角的大小.
如图所示,二面角α-l-β的面α内有一条直线AB,它与棱l的夹角为45°.AB与平面β所成的角为30°.求这个二面角的大小.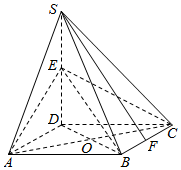 如图,四棱锥S-ABCD底面是正方形,SD⊥平面ABCD,SD=AD=2,点E是SD的中点,F是BC线段上的点,O是AC与BD的交点.
如图,四棱锥S-ABCD底面是正方形,SD⊥平面ABCD,SD=AD=2,点E是SD的中点,F是BC线段上的点,O是AC与BD的交点.