题目内容
【题目】如图,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成角为60°.
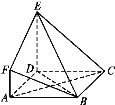
(1)求二面角F-BE-D的余弦值;
(2)设点M是线段BD上一个动点,试确定点M的位置,使得AM∥平面BEF,并证明你的结论.
【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】
(1)以D为原点建立空间直角坐标系,然后结合条件得到相关点的坐标,进而求得平面BEF的法向量![]() 和平面BDE的法向量
和平面BDE的法向量![]() ,求出两向量夹角的余弦值,再结合图形可得二面角的余弦值.(2)设点M(t,t,0),于是得
,求出两向量夹角的余弦值,再结合图形可得二面角的余弦值.(2)设点M(t,t,0),于是得![]() =(t-3,t,0),由AM∥平面BEF可得
=(t-3,t,0),由AM∥平面BEF可得![]() ,解得
,解得![]() ,故得点M坐标为(2,2,0),BM=
,故得点M坐标为(2,2,0),BM=![]() BD,即为所求.
BD,即为所求.
(1)因为DA,DC,DE两两垂直,所以建立空间直角坐标系D-xyz如图所示.
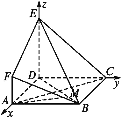
因为DE⊥平面ABCD,
所以BE与平面ABCD所成角为∠DBE,故∠DBE =60°,
所以![]() .
.
由AD=3可知DE=3![]() ,AF=
,AF=![]() .
.
则A(3,0,0),F(3,0,![]() ),E(0,0,3
),E(0,0,3![]() ),B(3,3,0),C(0,3,0),
),B(3,3,0),C(0,3,0),
所以![]() =(0,-3,
=(0,-3,![]() ),
),![]() =(3,0,-2
=(3,0,-2![]() ),
),
设平面BEF的法向量为![]() ,
,
则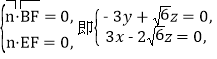
令z=![]() ,则
,则![]() .
.
同理得平面BDE的法向量为![]() ,(也可证AC⊥平面BDE,得
,(也可证AC⊥平面BDE,得![]() 即为法向量).
即为法向量).
所以cos<![]() ,
,![]() >=
>=![]() .
.
由图形得二面角F-BE-D为锐角,
所以二面角F-BE-D的余弦值为![]() .
.
(2)点M是线段BD上一个动点,设M(t,t,0).
则![]() =(t-3,t,0),
=(t-3,t,0),
因为AM∥平面BEF,
所以![]() ,
,
解得t=2.
此时,点M坐标为(2,2,0),BM=![]() BD,符合题意.
BD,符合题意.
所以当BM=![]() BD 时,满足AM∥平面BEF.
BD 时,满足AM∥平面BEF.

 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案【题目】4月23日是“世界读书日”,某中学在此期间开展了一系列的读书教育活动,为了解本校学生课外阅读情况,学校随机抽取了100名学生对其课外阅读时间进行调查,下面是根据调查结果绘制的学生日均课外阅读时间(单位:分钟)的频率分布直方图,若将日均课外阅读时间不低于60分钟的学生称为“读书谜”,低于60分钟的学生称为“非读书谜”

(1)求![]() 的值并估计全校3000名学生中读书谜大概有多少?(将频率视为概率)
的值并估计全校3000名学生中读书谜大概有多少?(将频率视为概率)
(2)根据已知条件完成下面2×2的列联表,并据此判断是否有99%的把握认为“读书谜”与性别有关?
非读书迷 | 读书迷 | 合计 | |
男 | 15 | ||
女 | 45 | ||
合计 |
附:![]() .
.
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
