题目内容
已知函数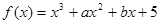 ,曲线
,曲线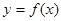 在点
在点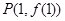 处的切线方程为
处的切线方程为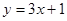 .
.
(1)求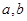 的值;
的值;
(2)求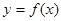 在
在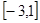 上的最大值.
上的最大值.
(1) ;(2)
;(2)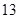 .
.
解析试题分析:(1)将切点 代入切线方程
代入切线方程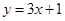 确定
确定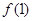 的值,求
的值,求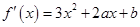 ,由切线方程
,由切线方程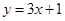 ,可知
,可知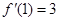 ,列出关于
,列出关于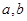 的方程组即可求解;(2)由(1)确定的
的方程组即可求解;(2)由(1)确定的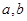 ,确定
,确定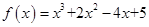 ,用导数确定
,用导数确定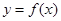 在区间
在区间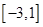 的极大值与极小值,然后比较极大值、端点值
的极大值与极小值,然后比较极大值、端点值 ,即可得到函数
,即可得到函数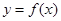 在区间
在区间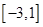 的最大值.
的最大值.
试题解析:(1)依题意可知点 为切点,代入切线方程
为切点,代入切线方程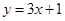 可得
可得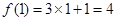
所以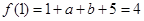 即
即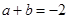
又由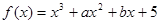 ,得
,得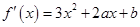
而由切线方程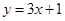 的斜率可知
的斜率可知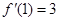
所以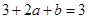 即
即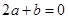
联立 7分
7分
解得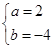 ,
,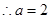 ,
,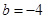 8分
8分
(2)由(1)知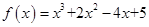 9分
9分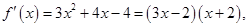 令
令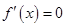 ,得
,得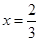 或
或 10分
10分
当 变化时,
变化时,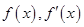 的变化如下表:
的变化如下表:

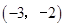
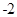
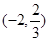

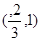
1 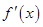
+ 0 - 0  练习册系列答案
练习册系列答案
江苏5年经典系列答案
初中毕业学业考试指导丛书系列答案
芒果教辅小学数学应用题系列答案
春雨教育小学数学图解巧练应用题系列答案
龙门书局系列答案
学而思小学数学秘籍系列答案
学林教育小学数学图解应用题系列答案
金博优题典单元练测活页卷系列答案
DIY英语系列答案
晨光全优口算应用题天天练系列答案
相关题目
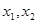
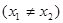 是函数
是函数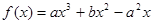 (
(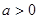 )的两个极值点
)的两个极值点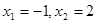 ,求函数
,求函数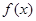 的解析式;
的解析式;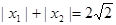 ,求
,求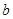 的最大值。
的最大值。 .
. (a为常数).
(a为常数).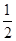 ,求证:当x∈(0,+∞)时,f(x)>1;
,求证:当x∈(0,+∞)时,f(x)>1; <e4(n∈N*)..
<e4(n∈N*)..