题目内容
19.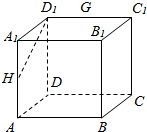 如图所示,在正方体ABCD-A1B1C1D1中,E、G、H分别是BC、C1D1、AA1、的中点.
如图所示,在正方体ABCD-A1B1C1D1中,E、G、H分别是BC、C1D1、AA1、的中点.(Ⅰ)求异面直线D1H与A1B所成角的余弦值
(Ⅱ)求证:EG∥平面BB1D1D.
分析 (Ⅰ)连接D1C和CH,可证A1B∥D1C,可得∠HD1C或其补角为异面直线D1H与A1B所成的角,设正方形边长为2,则在△D1HC中根据余弦定理可求cos∠HD1C的值,从而得解.
(Ⅱ)连接BD与AC交于点O,连接D1O,OE,GE,可证四边形OEGD1是平行四边形,即可证明$GE\underline{\underline{∥}}{D_1}O$,从而得证.
解答  解:(Ⅰ)连接D1C和CH,
解:(Ⅰ)连接D1C和CH,
∵A1D1$\underline{\underline{∥}}$B1C1$\underline{\underline{∥}}$BC,
∴四边形A1BCD1为平行四边形,
∴A1B∥D1C,
∴∠HD1C或其补角为异面直线D1H与A1B所成的角,…(3分)
∴设正方形边长为2,则在△D1HC中,${D_1}H=\sqrt{5},{D_1}C=2\sqrt{2},HC=3$,
根据余弦定理,$cos∠H{D_1}C=\frac{5+8-9}{{2×\sqrt{5}×2\sqrt{2}}}=\frac{{\sqrt{10}}}{10}$
则异面直线D1H与A1B所成的角的余弦值为$\frac{{\sqrt{10}}}{10}$…(7分)
(Ⅱ)证明 连接BD与AC交于点O,连接D1O,OE,GE,
∵$OE\underline{\underline{∥}}\frac{1}{2}CD,{D_1}G\underline{\underline{∥}}\frac{1}{2}CD$,
∴$OE\underline{\underline{∥}}{D_1}G$,
∴四边形OEGD1是平行四边形,…(9分)
∴$GE\underline{\underline{∥}}{D_1}O$,GE?面BB1D1D,D1O?面BB1D1D
∴EG∥面BB1D1D…(13分)
点评 本题主要考查了直线与平面垂直的判定,余弦定理的应用,考查了空间想象能力和推理论证能力,属于中档题.

 阅读快车系列答案
阅读快车系列答案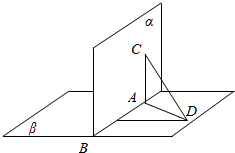 已知A,B,是直二面角α-l-β的棱上两点,线段AC?α,线段BD?β,且AC⊥l,BD⊥l,AC=12,AB=4,BD=3,求线段CD的长.
已知A,B,是直二面角α-l-β的棱上两点,线段AC?α,线段BD?β,且AC⊥l,BD⊥l,AC=12,AB=4,BD=3,求线段CD的长.