题目内容
10．已知不等式x2-（1+a）x+a＜0；（1）若该不等式的解集为（1，2），求a的值；
（2）若a∈R，解该不等式．
分析 （1）由于该不等式x2-（1+a）x+a＜0的解集为（1，2），可得1，2是一元二次方程x2-（1+a）x+a=0的两个实数根，利用根与系数的关系即可得出．
（2）x2-（1+a）x+a＜0，化为（x-a）（x-1）＜0，对a分类讨论即可得出．
解答 解：（1）∵该不等式x2-（1+a）x+a＜0的解集为（1，2），
∴1，2是一元二次方程x2-（1+a）x+a=0的两个实数根，
∴1+2=1+a，1×2=a，
解得a=2．
（2）x2-（1+a）x+a＜0，化为（x-a）（x-1）＜0，
当a＜1时，解得a＜x＜1，因此不等式解集为（a，1）；
当a=1时，解集为∅；
当a＞1，解得1＜x＜a，因此不等式解集为（1，a）．
点评 本题考查了一元二次不等式的解法、一元二次方程的根与系数的关系、分类讨论方法，考查了推理能力与计算能力，属于中档题．
练习册系列答案
夺冠训练单元期末冲刺100分系列答案
新思维小冠军100分作业本系列答案
名师指导一卷通系列答案
相关题目
15．i是虚数单位，复数$\frac{i}{2+i}$=（ ）
| A． | $\frac{-1+2i}{3}$ | B． | $\frac{1+2i}{3}$ | C． | $\frac{1+2i}{5}$ | D． | $\frac{-1+2i}{5}$ |
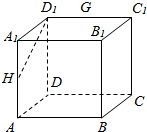如图所示，在正方体ABCD-A1B1C1D1中，E、G、H分别是BC、C1D1、AA1、的中点．