题目内容
如图,抛物线关于 轴对称,它的顶点在坐标原点,点P(1,2),
轴对称,它的顶点在坐标原点,点P(1,2), ,
,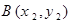 均在抛物线上.
均在抛物线上.

(1)求该抛物线方程;
(2)若AB的中点坐标为 ,求直线AB方程.
,求直线AB方程.
 轴对称,它的顶点在坐标原点,点P(1,2),
轴对称,它的顶点在坐标原点,点P(1,2), ,
,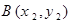 均在抛物线上.
均在抛物线上.
(1)求该抛物线方程;
(2)若AB的中点坐标为
 ,求直线AB方程.
,求直线AB方程.(1) ;(2)
;(2) .
.
 ;(2)
;(2) .
.试题分析:(1)这里求出的是抛物线的标准方程,可设为
 ,
, 点坐标代入即求得;(2)已知弦
点坐标代入即求得;(2)已知弦 中点坐标,可把
中点坐标,可把 两点坐标
两点坐标 ,
, 直接代入抛物线方程,所得两式相减就能求出直线
直接代入抛物线方程,所得两式相减就能求出直线 的斜率,从而得直线方程.
的斜率,从而得直线方程.试题解析:(1)设抛物线方程为
 ,把
,把 点坐标代入得
点坐标代入得 ,
, ,
,∴抛物线方程为
 ;
;(2)∵
 ,
, 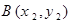 均在抛物线上,
均在抛物线上,∴
 ,
, ,
,两式相减得:
 ,
,AB的中点坐标为
 ,所以
,所以 ,
,∴
 ,
,∴直线
 方程为
方程为 ,即
,即 .
.
练习册系列答案
相关题目
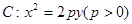 的焦点为
的焦点为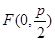 ,准线为
,准线为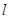 ,点
,点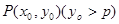 为抛物线C上的一点,且
为抛物线C上的一点,且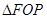 的外接圆圆心到准线的距离为
的外接圆圆心到准线的距离为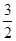 .
.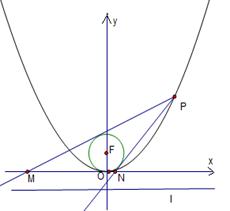
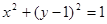 ,过点P作圆F的2条切线分别交
,过点P作圆F的2条切线分别交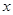 轴于点
轴于点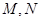 ,求
,求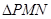 面积的最小值时
面积的最小值时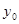 的值.
的值.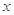 轴上,离心率为
轴上,离心率为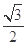 ,长轴长为
,长轴长为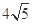 ,直线
,直线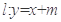 交椭圆于不同的两点
交椭圆于不同的两点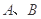 .
.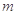 的取值范围;
的取值范围;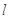 不经过椭圆上的点
不经过椭圆上的点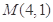 ,求证:直线
,求证:直线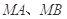 的斜率互为相反数.
的斜率互为相反数. 中,已知中心在原点,离心率为
中,已知中心在原点,离心率为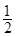 的椭圆E的一个焦点为圆
的椭圆E的一个焦点为圆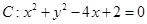 的圆心.
的圆心.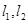 ,当直线
,当直线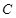 相切时,求P点坐标.
相切时,求P点坐标.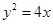 焦点
焦点 的直线
的直线 与抛物线相交于
与抛物线相交于 两点,若
两点,若 ,则
,则 .
.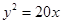 的焦点为圆心,且与双曲线
的焦点为圆心,且与双曲线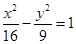 的两条渐近线都相切的圆的方程为 .
的两条渐近线都相切的圆的方程为 . ,椭圆E的内接平行四边形的一组对边分别经过它的两个焦点(如图),则这个平行四边形面积的最大值是 .
,椭圆E的内接平行四边形的一组对边分别经过它的两个焦点(如图),则这个平行四边形面积的最大值是 .
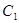 与双曲线
与双曲线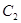 有共同的焦点
有共同的焦点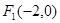 ,
,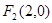 ,椭圆的一个短轴端点为
,椭圆的一个短轴端点为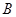 ,直线
,直线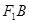 与双曲线的一条渐近线平行,椭圆
与双曲线的一条渐近线平行,椭圆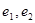 ,则
,则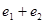 取值范围为( )
取值范围为( )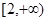
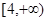
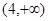

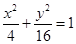 },B={(x,y)|y=3x},则A∩B的子集的个数是( )
},B={(x,y)|y=3x},则A∩B的子集的个数是( )