题目内容
在正四棱柱ABCD-A1B1C1D1中，E为CC1的中点．（1）求证：AC1∥平面BDE；
（2）求异面直线A1E与BD所成角．
分析：（1）利用线面平行的判定定理证明．
（2）利用异面直线所成角的定义求空间角．
（2）利用异面直线所成角的定义求空间角．
解答：
解：（1）连结AC交BD于O，连接EO
因为平行四边形ABCD，
所以O为BD中点，E为CC1中点
所以OE为△AC1C中位线，
所以OE∥AC1-----------3
OE?面BDE
AC1?面BDE
AC1∥面BDE------------6
（2）因正四棱柱ABCD-A1B1C1D1
所以BD⊥A1A，又因BD⊥AC
A1A∩AC=AA1A?面A1AC C1
AC?面A1ACC1
所以BD⊥面A1ACC1----------------9
A1E?面A1ACC1
所以BD⊥A1E，
A1E与BD所成角为900----------12
解：（1）连结AC交BD于O，连接EO因为平行四边形ABCD，
所以O为BD中点，E为CC1中点
所以OE为△AC1C中位线，
所以OE∥AC1-----------3
OE?面BDE
AC1?面BDE
AC1∥面BDE------------6
（2）因正四棱柱ABCD-A1B1C1D1
所以BD⊥A1A，又因BD⊥AC
A1A∩AC=AA1A?面A1AC C1
AC?面A1ACC1
所以BD⊥面A1ACC1----------------9
A1E?面A1ACC1
所以BD⊥A1E，
A1E与BD所成角为900----------12
点评：本题主要考查直线和平面平行的判定依据空间异面直线所成的角，要求熟练掌握相关的定理．
练习册系列答案
相关题目
如图，在正四棱柱ABCD-A1B1C1D1中，棱长AA1=2，AB=1，E是AA1的中点．
在正四棱柱ABCD-A1B1C1D1中，AA1=2AB，E为CC1的中点．
如图，在正四棱柱ABCD-A1B1C1D1中，AB=1，AA1=2，M、N分别为B1B和A1D的中点．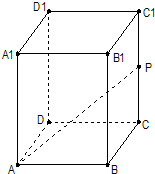
（2012•长宁区一模）在正四棱柱ABCD-A1B1C1D1中，已知底面ABCD的边长为2，点P是CC1的中点，直线AP与平面BCC1B1成30°角，求异面直线BC1和AP所成角的大小．（结果用反三角函数值表示）
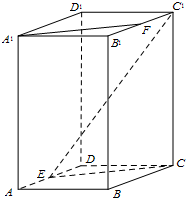（2012•昌平区二模）在正四棱柱ABCD-A1B1C1D1中，E为AD中点，F为B1C1中点．