题目内容
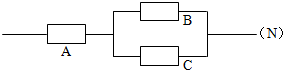
19.如图,用A、B、C三类不同的元件连接成两个系统N1、N2,当元件A、B、C都正常工作时,系统N1正常工作;当元件A正常工作且元件B、C至少有一个正常工作时,系统N2正常工作.已知元件A、B、C正常工作的概率依次为0.80,0.90,0.90.分别求系统N1、N2正常工作的概率P1、P2.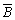
19.本小题考查相互独立事件同时发生或互斥事件有一个发生的概率的计算方法,考查运用概率知识解决实际问题的能力.
解:分别记元件A、B、C正常工作为事件A、B、C,由已知条件P(A)= 0.80,P(B)= 0.90,
P(C)= 0.90.
(Ⅰ)因为事件A、B、C是相互独立的,所以,系统N1正常工作的概率
P1= P(A·B·C)
= P(A)·P(B)·P(C)
= 0.80×0.90×0.90 = 0.648.
故系统N1正常工作的概率为0.648.
(Ⅱ)系统N2正常工作的概率
P2 = P(A)·[1-P(![]() ·
·![]() )]=P(A)·[1-P(
)]=P(A)·[1-P(![]() )·P(
)·P(![]() )],
)],
∵ P(![]() )=1-P(B)=1-0.90 = 0.10,
)=1-P(B)=1-0.90 = 0.10,
P(![]() )=1-P(C)= 1-0.90 = 0.10,
)=1-P(C)= 1-0.90 = 0.10,
∴ P2 = 0.80×[1―0.10×0.10]= 0.80×0.99 = 0.792.
故系统N2正常工作的概率为0.792.

练习册系列答案
相关题目

 如图所示,直三棱柱ABC-A1B1C1中,AB⊥AC,D,E分别为AA1,B1C的中点,若记
如图所示,直三棱柱ABC-A1B1C1中,AB⊥AC,D,E分别为AA1,B1C的中点,若记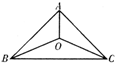 三个城市分别位于A,B,C三点处(如图),且
三个城市分别位于A,B,C三点处(如图),且 斜三棱柱OAB-CA1B1,其中向量
斜三棱柱OAB-CA1B1,其中向量