题目内容
已知函数
．
①若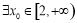
，使
成立，则实数
的取值范围为 ；
②若
，
使得
，则实数
的取值范围为 ．
①
；②
．
【解析】
试题分析: ①因为
，当且仅当
即
时等号成立，所以
的值域为
，又
，
所以
；
②
，
使得
等价于
，由①可知
，
在区间
上是增函数，所以
，由
和
得
.
考点：基本不等式、指数函数性质.
练习册系列答案
轻松暑假总复习系列答案
相关题目
轻松暑假总复习系列答案题目内容
已知函数．
①若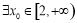，使成立，则实数的取值范围为 ；
②若，使得，则实数的取值范围为 ．
①；②．
【解析】
试题分析: ①因为，当且仅当即时等号成立，所以的值域为，又，所以；
②，使得等价于，由①可知，在区间上是增函数，所以，由和得.
考点：基本不等式、指数函数性质.
轻松暑假总复习系列答案
作圆
的两条切线，切点分别为A、B，则直线AB的方程为
B.
D.
是虚数单位，则复数
的虚部是（ ）
C.
D.1
的正方形的四棱锥
中，已知
，且
，则直线
与平面
所成的角的余弦值为（ ）
B.
C.
D.
，点
，P是圆E上任意一点．线段PF的垂直平分线和半径PE相交于Q．
的方程；
与(Ⅰ)中轨迹
相交于
两点，直线
的斜率分别为
．△
的面积为
，以
为直径的圆的面积分别为
．若
恰好构成等比数列，求
的取值范围．
∶
∶
∶
∶
，则角
．
若
，则函数
在区间
内 
，
的蔡查罗和（蔡查罗是一位数学家）定义为
，其中
．若一个99项的数列（
的蔡查罗和为1000，那么100项数列
的蔡查罗和为