题目内容
10. 如图,在三棱锥S-ABC中,SA⊥平面ABC,∠ABC=90°,SA=BC=2,AB=4,M,N,D分别是SC,AB,BC的中点.
如图,在三棱锥S-ABC中,SA⊥平面ABC,∠ABC=90°,SA=BC=2,AB=4,M,N,D分别是SC,AB,BC的中点.(1)求证:MN⊥AB;
(2)求二面角S-ND-B的余弦值;
(3)求点M到平面SND的距离.
分析 (1)取AC的中点E,连接ME,NE.则ME∥SA,由线面垂直得ME⊥AB,由直角性质得NE⊥AB,从而AB⊥平面MNE,由此能证明MN⊥AB.
(2)过A作AF⊥DN且与DN的延长线相交于点F,连接SF,由已知得∠SFA是二面角S-ND-A的平面角,也是二面角S-ND-B的平面角的补角,由此能示出二面角S-ND-B的余弦值.(3)过点A作AH⊥SF于H,由已知得AH的长为点A到平面SND的距离,点M到平面SND的距离是点C到平面SND的距离的$\frac{1}{2}$倍,点C到平面SND的距离等于点A到平面SND的距离,由此能求出点M到平面SND的距离.
解答 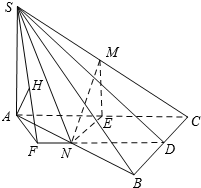 (本题满分14分)
(本题满分14分)
(1)证明:取AC的中点E,连接ME,NE.则ME∥SA,
又SA⊥平面ABC,∴ME⊥平面ABC.
∵AB?平面ABC,∴ME⊥AB.(1分)
∵N,E分别为AB,AC的中点,∴NE∥BC.
∵∠ABC=90°,即AB⊥BC,∴NE⊥AB.
∵ME∩NE=E,ME?平面MNE,NE?平面MNE,
∴AB⊥平面MNE.(3分)
∵MN?平面MNE,∴MN⊥AB.(4分)
(2)解:过A作AF⊥DN且与DN的延长线相交于点F,连接SF
∵SA⊥DF,AF⊥DF,SA∩AF=A,∴DF⊥平面SAF,∴DF⊥SF
∴∠SFA是二面角S-ND-A的平面角,也是二面角S-ND-B的平面角的补角,----(7分)
在Rt△DBN中,$ND=\sqrt{D{B^2}+N{B^2}}=\sqrt{5}$,$sin∠DNB=\frac{DB}{ND}=\frac{{\sqrt{5}}}{5}$.
在Rt△AFN中,AF=AN$sin∠ANF=2×\frac{{\sqrt{5}}}{5}=\frac{{2\sqrt{5}}}{5}$.
在Rt△SAF中,$SF=\sqrt{S{A^2}+A{F^2}}$=$\frac{{2\sqrt{30}}}{5}$,$cos∠AFS=\frac{AF}{SF}=\frac{{\sqrt{6}}}{6}$.
∴二面角S-ND-B的余弦值为$-\frac{{\sqrt{6}}}{6}$.(10分)
(3)解:过点A作AH⊥SF于H,
由(2)知平面SAF⊥平面SND,且平面SAF∩平面SND=SF,
∴AH⊥平面SND.∴AH的长为点A到平面SND的距离.
在Rt△AFN中,$AH=\frac{SA•AF}{SF}$=$\frac{{\sqrt{6}}}{3}$.(12分)
∵点M是SC的中点,∴点M到平面SND的距离是点C到平面SND的距离的$\frac{1}{2}$倍.
∵AC∥ND,∴AC∥平面SND.
∴点C到平面SND的距离等于点A到平面SND的距离.
∴点M到平面SND的距离是$\frac{{\sqrt{6}}}{6}$.(14分)
点评 本题考查异面直线垂直的证明,考查二面角的余弦值的求法,考查点到平面的距离的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | 1 | B. | -1 | C. | $\frac{1}{3}$ | D. | -$\frac{1}{3}$ |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | (-$\frac{3}{2}$,1)和$\frac{19}{4}$ | B. | (3,2)和$\frac{\sqrt{19}}{2}$ | C. | (-$\frac{3}{2}$,1)和$\frac{\sqrt{19}}{2}$ | D. | ($\frac{3}{2}$,-1)和$\frac{\sqrt{19}}{2}$ |
 在空间四边形ABCD中,设AB⊥CD,AC⊥BD.
在空间四边形ABCD中,设AB⊥CD,AC⊥BD.