题目内容
【题目】设![]() 、
、![]() 分别是椭圆
分别是椭圆![]() 的左、右焦点.
的左、右焦点.
(1)若![]() 是该椭圆上的一个动点,求
是该椭圆上的一个动点,求![]() 的最大值与最小值.
的最大值与最小值.
(2)是否存在过点![]() 的直线
的直线![]() 与椭圆交于不同的两点
与椭圆交于不同的两点![]() ,使得
,使得![]() ?若存在,求直线
?若存在,求直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
【答案】(1)最小值3,最大值4;(2)不存在
【解析】
试题(1)将数量积转化为坐标表示,利用坐标的有界性求出最值;(2)设出直线方程,根据|F2C|=|F2D|,可知F2在弦CD的中垂线上,利用中点和斜率关系,写出中垂线方程,代入F2点即可判断.或者根据焦半径公式判断更为简洁.
试题解析:(1)易知a=![]() ,b=2,c=1,∴F1(-1,0),F2(1,0)
,b=2,c=1,∴F1(-1,0),F2(1,0)
设P(x,y),则![]()
![]() =(-1-x,-y)·(1-x,-y)
=(-1-x,-y)·(1-x,-y)
=x2+y2-1
=x2+4-![]() x2-1
x2-1
=![]() x2+3
x2+3
∵x2∈[0,5],
当x=0,即点P为椭圆短轴端点时,![]() 有最小值3;
有最小值3;
当x=±![]() ,即点P为椭圆长轴端点时,
,即点P为椭圆长轴端点时,![]() 有最大值4.
有最大值4.
(2)法一、假设存在满足条件的直线l,易知点A(5,0)在椭圆外部,当直线斜率不存在时,直线l与椭圆无交点.
所以满足条件的直线斜率存在,设为k
则直线方程为y=k(x-5)
由方程组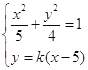
得:(5k2+4)x2-50k2x+125k2-20=0
依题意,△=20(16-80k2)>0
得:![]()
当![]() 时,设交点为C(x1,y1),D(x2,y2),CD中点为R(x0,y0)
时,设交点为C(x1,y1),D(x2,y2),CD中点为R(x0,y0)
则x1+x2=![]() ,x0=
,x0=![]()
∴y0=k(x0-5)=k(![]() -5)=
-5)=![]()
又|F2C|=|F2D|,有F2R⊥l,即![]() =-1
=-1
即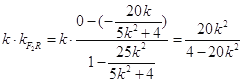 =-1
=-1
即20k2=20k2-4,
该等式不成立,所以满足条件的直线l不存在.
法二、设交点为C(x1,y1),D(x2,y2),
设它们到右准线x=![]() 的距离分别为d1、d2,
的距离分别为d1、d2,
根据椭圆第二定义,有![]()
因为|F2C|=|F2D|,故d1=d2,于是x1=x2,
于是CD所在直线l⊥x轴
又直线l经过A(5,0)点,于是l的方程为x=5
但x=5与椭圆无公共点,所以,满足条件的直线不存在.

 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案