题目内容
直线
与曲线
的交点个数为（ ）
| A．0 | B．1 | C．2 | D．3 |
B.
解析试题分析：根据曲线的方程可分两种情况讨论：（1）当
时，联立曲线方程
与直线得：
，应舍去；（2）当
时，联立曲线方程与直线得：
.
考点：直线与曲线的综合应用.
练习册系列答案
相关题目
的顶点坐标
，直角顶点
，顶点
在
轴上，点
为线段
的中点
边所在直线方程；（2）圆
是△ABC的外接圆，求圆
是否是定值？在椭圆
上有两个动点
，
为定点，
，则
的最小值为（ ）
| A．6 | B． | C．9 | D． |
若双曲线
的离心率为2,则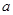
等于（ ）
A． | B． | C． | D．1 |
=1（a>0，b>0）的右焦点是抛物线y2=8x的焦点F，两曲线的一个公共点为P，且|PF| =5，则此双曲线的离心率为（ ）
已知双曲线
的虚轴长是实轴长的2倍，则实数
的值是( )
A． | B． | C． | D． |
已知抛物线C：
的焦点为
,
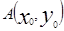是C上一点，
，则
（ ）
| A． 1 | B． 2 | C． 4 | D． 8 |
从椭圆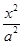
＋
＝1(a>b>0)上一点P向x轴作垂线，垂足恰为左焦点F1，A是椭圆与x轴正半轴的交点，B是椭圆与y轴正半轴的交点，且AB∥OP(O是坐标原点)，则该椭圆的离心率是( )
A． | B． | C． | D． |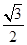
若椭圆
＋
＝1与双曲线
－
＝1(m，n，p，q均为正数)有共同的焦点F1，F2，P是两曲线的一个公共点，则
·
＝( )
| A．p2－m2 | B．p－m | C．m－p | D．m2－p2 |