题目内容
设ABCD-A1B1C1D1是平行六面体，M是底面ABCD的中心，N是侧面BCC1B1对角线BC1上的点，且BN=3NC1，设| MN |
| AB |
| AD |
| AA1 |
分析：利用向量的运算法则：三角形法则、平行四边形法则表示出
，即可求得a，b，c的值．
| MN |
解答：解：∵
=
+
=
+
=
(
-
) +
(
+
)
=
+
+
∴a=
，b=
，c=
．
| MN |
| MB |
| BN |
=
| 1 |
| 2 |
| DB |
| 3 |
| 4 |
| BC1 |
=
| 1 |
| 2 |
| AB |
| AD |
| 3 |
| 4 |
| BB1 |
| BC |
=
| 1 |
| 2 |
| AB |
| 1 |
| 4 |
| AD |
| 3 |
| 4 |
| AA1 |
∴a=
| 1 |
| 2 |
| 1 |
| 4 |
| 3 |
| 4 |
点评：本题考查利用向量的运算法则将未知的向量用已知的基底表示从而能将未知向量间的问题转化为基底间的关系解决，将要求向量放到封闭图形中，利用向量加法的三角形法则即可求解，属基础题．
练习册系列答案
相关题目
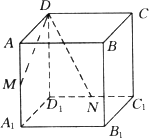
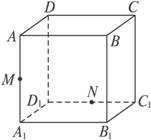
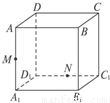
如图，在棱长为a的正方体ABCD-A1B1C1D1中，M、N分别是AA1、D1C1的中点，过D、M、N三点的平面与正方体的下底面相交于直线l；
