题目内容
如图，在棱长为a的正方体ABCD－A1B1C1D1中，M、N分别是AA1、D1C1的中点，过D、M、N三点的平面与正方体的下底面相交于直线l，
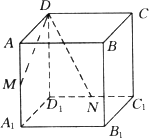
(1)画出l的位置；
(2)设l∩A1B1＝P，求PB1的长．
答案：
解析：
解析：
|
解：(1)如图所示，平面DMN与平面AD1的交线为DM，设DM∩D1A1＝Q，连结QN，则平面DMN与平面A1C1的交线为QN，QN即为所求作的直线l． (2)设QN∩A1B1＝P． ∵△MA1Q≌△MAD， ∴A1Q＝AD＝a＝A1D1． ∴A1是QD1的中点．
|
练习册系列答案
名师点拨卷系列答案
英才计划期末调研系列答案
相关题目
如图，在棱长为2的正四面体A-BCD中，若以△ABC为视角正面，则其正视图的面积是（ ）
，当
取什么位置时，三棱柱的体积最大？
，AG＝
，给出下列四个命题：①AC⊥BD，②FG＝
，③侧面与底面所成二面角的余弦值为
，④
，其中真命题的序号是（ ）
