题目内容
△ABC满足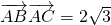 ,∠BAC=30°,设M是△ABC内的一点,S△MBC=
,∠BAC=30°,设M是△ABC内的一点,S△MBC= ,S△MCA=x,S△MAB=y,则
,S△MCA=x,S△MAB=y,则 的最小值为________.
的最小值为________.
18
分析:根据题意求得|AC|•|AB|进而利用三角形面积公式求得△ABC的面积,然后根据S△MBC推断M在三角形中位线上,进而求得S△MCA+S△MAB的值,即x+y的值,代入 中整理成基本不等式的形式,求得其最小值.
中整理成基本不等式的形式,求得其最小值.
解答:∵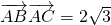 ,∠BAC=30°
,∠BAC=30°
∴|AC|•|AB|=4,
又S△ABC= •AC•AB•sin∠BAC=1 S△MBC=
•AC•AB•sin∠BAC=1 S△MBC=
∴M在三角形中位线上
S△MCA+S△MAB=x+y= ,即1=2(x+y)
,即1=2(x+y)
∴ =
= =10+
=10+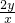 +
+ ≥10+2
≥10+2 =18
=18
故答案为18.
点评:本题主要考查了基本不等式在最值问题中的应用.解题的关键是拼凑出基本不等式的形式.
分析:根据题意求得|AC|•|AB|进而利用三角形面积公式求得△ABC的面积,然后根据S△MBC推断M在三角形中位线上,进而求得S△MCA+S△MAB的值,即x+y的值,代入
 中整理成基本不等式的形式,求得其最小值.
中整理成基本不等式的形式,求得其最小值.解答:∵
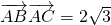 ,∠BAC=30°
,∠BAC=30°∴|AC|•|AB|=4,
又S△ABC=
 •AC•AB•sin∠BAC=1 S△MBC=
•AC•AB•sin∠BAC=1 S△MBC=
∴M在三角形中位线上
S△MCA+S△MAB=x+y=
 ,即1=2(x+y)
,即1=2(x+y) ∴
 =
= =10+
=10+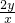 +
+ ≥10+2
≥10+2 =18
=18故答案为18.
点评:本题主要考查了基本不等式在最值问题中的应用.解题的关键是拼凑出基本不等式的形式.

练习册系列答案
相关题目
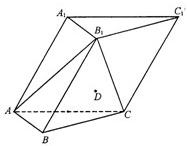 如图,在各棱长均为2的三棱柱ABC-A1B1C1中,侧面A1ACC1⊥底面ABC,∠A1AC=60°.
如图,在各棱长均为2的三棱柱ABC-A1B1C1中,侧面A1ACC1⊥底面ABC,∠A1AC=60°.