题目内容
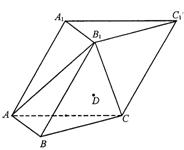
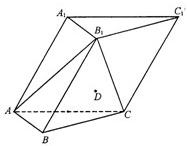 如图,在各棱长均为2的三棱柱ABC-A1B1C1中,侧面A1ACC1⊥底面ABC,∠A1AC=60°.
如图,在各棱长均为2的三棱柱ABC-A1B1C1中,侧面A1ACC1⊥底面ABC,∠A1AC=60°.(Ⅰ)求侧棱AA1与平面AB1C所成角的正弦值的大小;
(Ⅱ)已知点D满足
| BD |
| BA |
| BC |
分析:(Ⅰ)建立空间直角坐标系,求出AA1向量,平面AA1C1C的法向量,然后求出侧棱AA1与平面AB1C所成角的正弦值的大小;
(Ⅱ)在(Ⅰ)的前提下,求出
=
+
,设出P的坐标,使DP∥平面AB1C,即
与法向量共线,再求出P的坐标.
(Ⅱ)在(Ⅰ)的前提下,求出
| BD |
| BA |
| BC |
| DP |
解答:解:(Ⅰ)∵侧面A1ACC1⊥底面ABC,作A1O⊥AC于点O,
∴A1O⊥平面ABC.又∠ABC=∠A1AC=60°,且各棱长都相等,
∴AO=1,OA1=OB=
,BO⊥AC.(2分)
故以O为坐标原点,建立如图所示的空间直角坐标系O-xyz,则
A(0,-1,0),B(
,0,0),A1(0,0,
),
C(0,1,0),
=(0,1,
);
∴
=(
,2,
),
=(0,2,0).(4分)
设平面AB1C的法向量为n=(x,y,1)
则
解得n=(-1,0,1).(6分)
由cos<
,n>=
=
=
.
而侧棱AA1与平面AB1C所成角,
即是向量
与平面AB1C的法向量所成锐角的余角,
∴侧棱AA1与平面AB1C所成角的正弦值的大小为
.(6分)
(Ⅱ)∵
=
+
,
而
=(-
,-1,0),
=(-
,1,0).
∴
=(-2
,0,0).(8分)
又∵B(
,0,0),∴点D的坐标为D(-
,0,0).
假设存在点P符合题意,则点P的坐标可设为P(0,y,z).
∴
=(
,y,z)
∵DP∥平面AB1C,n=(-1,0,1)为平面AB1C的法向量,
∴由
=λ
,得
,∴y=0.(11分)
又DP?平面AB1C,
故存在点P,使DP∥平面AB1C,其坐标为(0,0,
),即恰好为A1点.(12分)
∴A1O⊥平面ABC.又∠ABC=∠A1AC=60°,且各棱长都相等,
∴AO=1,OA1=OB=
| 3 |
故以O为坐标原点,建立如图所示的空间直角坐标系O-xyz,则
A(0,-1,0),B(
| 3 |
| 3 |
C(0,1,0),
| AA1 |
| 3 |
∴
A
|
| 3 |
| 3 |
| AC |
设平面AB1C的法向量为n=(x,y,1)
则
|
解得n=(-1,0,1).(6分)
由cos<
| AA1 |
| ||||
|
|
| ||
2
|
| ||
| 4 |
而侧棱AA1与平面AB1C所成角,
即是向量
| AA1 |
∴侧棱AA1与平面AB1C所成角的正弦值的大小为
| ||
| 4 |
(Ⅱ)∵
| BD |
| BA |
| BC |
而
| BA |
| 3 |
| BC |
| 3 |
∴
| BD |
| 3 |
又∵B(
| 3 |
| 3 |
假设存在点P符合题意,则点P的坐标可设为P(0,y,z).
∴
| DP |
| 3 |
∵DP∥平面AB1C,n=(-1,0,1)为平面AB1C的法向量,
∴由
| AP |
| AA1 |
|
又DP?平面AB1C,
故存在点P,使DP∥平面AB1C,其坐标为(0,0,
| 3 |
点评:本题考查棱柱的结构特征,考查空间想象能力,逻辑思维能力,具有探索性特点,是难度较大题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 B
B ,在直线AA
,在直线AA
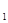 B
B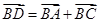 ,在直线AA
,在直线AA