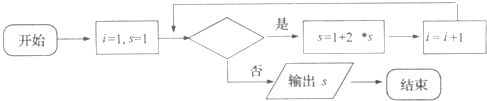
题目内容
【题目】如图,三棱柱ABC﹣A1B1C1中,点A1在平面ABC内的射影O为AC的中点,A1O=2,AB⊥BC,AB=BC= ![]() 点P在线段A1B上,且cos∠PAO=
点P在线段A1B上,且cos∠PAO= ![]() ,则直线AP与平面A1AC所成角的正弦值为 .
,则直线AP与平面A1AC所成角的正弦值为 . 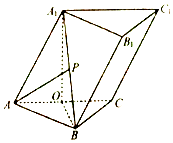
【答案】![]()
【解析】解:∵AB⊥BC,AB=BC= ![]() ,∴AC=2,AO=1. ∵点A1在平面ABC内的射影O为AC的中点,A1O=2,AB⊥BC,
,∴AC=2,AO=1. ∵点A1在平面ABC内的射影O为AC的中点,A1O=2,AB⊥BC,
∴AO,BO,A1O互相垂直,即面ABC,面AA1C,面A1OB互相垂直,
取AA1的中点H,连结PO,PH,AN.则PH⊥面AA1C
△APO为直角三角形,且cos∠PAO= ![]() ,∴AP=
,∴AP= ![]() ,
,
∠PAH为直线AP与平面A1AC所成角,sin∠PAH= ![]() .
.
所以答案是: ![]()

【考点精析】解答此题的关键在于理解空间角的异面直线所成的角的相关知识,掌握已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则 .
.

练习册系列答案
 英才计划期末调研系列答案
英才计划期末调研系列答案 精英口算卡系列答案
精英口算卡系列答案
相关题目