题目内容
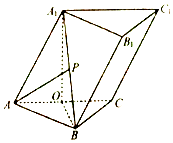
【题目】如图,多面体ABCDPE的底面ABCD是平行四边形,AD=AB=2, ![]()
![]() =0,PD⊥平面ABCD,EC∥PD,且PD=2EC=2,则二面角A﹣PB﹣E的大小为( )
=0,PD⊥平面ABCD,EC∥PD,且PD=2EC=2,则二面角A﹣PB﹣E的大小为( ) 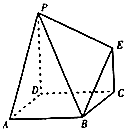
A.![]()
B.![]()
C.![]()
D.![]()
【答案】D
【解析】解:由 ![]()
![]() =0,PD⊥平面ABCD, 可得:PD⊥DA,PD⊥DC,AD⊥DC,
=0,PD⊥平面ABCD, 可得:PD⊥DA,PD⊥DC,AD⊥DC,
分别以DA、DC、DP所在直线为x、y、z轴建立空间直角坐标系,
∵AD=AB=2,PD=2EC=2,
∴A(2,0,0),B(2,2,0),P(0,0,2),E(0,2,1),![]() ,
, ![]() ,
, ![]() .
.
设平面PAB的一个法向量为 ![]() =(x,y,z),
=(x,y,z),
由 ![]() ,取z=1,得
,取z=1,得 ![]() ;
;
设平面PEB的一个法向量为 ![]() =(a,b,c),
=(a,b,c),
由 ![]() ,取c=2,得
,取c=2,得 ![]() .
.
∴cos< ![]() >=
>= ![]() =
= ![]() .
.
∴二面角A﹣PB﹣E的大小为 ![]() .
.
故选:D.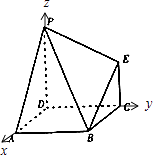

练习册系列答案
相关题目