题目内容
已知函数 ,m∈R.
,m∈R.
(1)若 ,求证:函数f(x)是R上的奇函数;
,求证:函数f(x)是R上的奇函数;
(2)若函数f(x)在区间(1,2)没有零点,求实数m的取值范围.
解:(1 )定义域为R关于原点对称.因为
f(x)+f(-x)= +
+ =
= +
+ =0,
=0,
所以函数f(x)是定义在R上的奇函数.
(2)f'(x)=- <0,
<0,
∴f(x)是实数集R上的单调递减函数(不说明单调性扣2分)
又函数f(x)的图象不间断,在区间(1,2)恰有一个零点,有f(1)f(2)<0
即(m+ )(m+
)(m+ )<0解之得-
)<0解之得- <m<-
<m<- ,故函数
,故函数
f(x)在区间(1,2)没有零点时,实数m的取值范围是m≥- 或m≤-
或m≤- …
…
分析:(1)利用奇函数的定义,考察f(-x)=-f(x)或f(x)+f(-x)=0在定义域内是否恒成立,若是则为奇函数,否则不是奇函数.
(2)求导函数,确定f(x)的单调性,要使函数f(x)在区间(1,2)上没有零点,先考察其对立面即在区间(1,2)恰有一个零点时m的取值范围,最后由此求补集即可求得所求实数m的取值范围.
点评:本题考查函数奇偶性的判断,考查导数知识的运用,考查函数的零点,考查不等式的解,属于中档题.
f(x)+f(-x)=
 +
+ =
= +
+ =0,
=0,所以函数f(x)是定义在R上的奇函数.
(2)f'(x)=-
 <0,
<0,∴f(x)是实数集R上的单调递减函数(不说明单调性扣2分)
又函数f(x)的图象不间断,在区间(1,2)恰有一个零点,有f(1)f(2)<0
即(m+
 )(m+
)(m+ )<0解之得-
)<0解之得- <m<-
<m<- ,故函数
,故函数f(x)在区间(1,2)没有零点时,实数m的取值范围是m≥-
 或m≤-
或m≤- …
…分析:(1)利用奇函数的定义,考察f(-x)=-f(x)或f(x)+f(-x)=0在定义域内是否恒成立,若是则为奇函数,否则不是奇函数.
(2)求导函数,确定f(x)的单调性,要使函数f(x)在区间(1,2)上没有零点,先考察其对立面即在区间(1,2)恰有一个零点时m的取值范围,最后由此求补集即可求得所求实数m的取值范围.
点评:本题考查函数奇偶性的判断,考查导数知识的运用,考查函数的零点,考查不等式的解,属于中档题.

练习册系列答案
相关题目
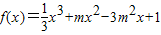 ,m∈R.
,m∈R. ,m∈R.
,m∈R.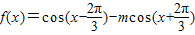 (m∈R)的图象经过点p(0,0)
(m∈R)的图象经过点p(0,0)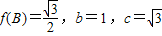 ,且a>b,试判断△ABC的形状,并说明理由.
,且a>b,试判断△ABC的形状,并说明理由. ,m∈R.
,m∈R.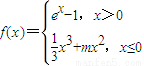 (m∈R,e是自然常数).
(m∈R,e是自然常数).