题目内容
已知函数 ,m∈R.
,m∈R.(Ⅰ)求f(x)的极值;
(Ⅱ)若lnx-ax<0在(0,+∞)上恒成立,求a的取值范围.
【答案】分析:(1)由导数运算法则知, ,再利用导数与单调性关系解得即可;
,再利用导数与单调性关系解得即可;
(2)存在性问题,只需等价于只需 在(0,+∞)上的最大值小于a即可,函数的最值问题利用导数解决.
在(0,+∞)上的最大值小于a即可,函数的最值问题利用导数解决.
解答:解:(Ⅰ)由导数运算法则知, .
.
令f'(x)=0,得x=em.(3分)
当x∈(0,em)时,f'(x)>0,f(x)单调递增;
当x∈(em,+∞)时,f'(x)<0,f(x)单调递减.
故当x=em时,f(x)有极大值,且极大值为f(em)=e-m.(6分)
(Ⅱ)欲使lnx-ax<0在(0,+∞)上恒成立,只需 在(0,+∞)上恒成立,
在(0,+∞)上恒成立,
等价于只需 在(0,+∞)上的最大值小于a.(9分)
在(0,+∞)上的最大值小于a.(9分)
设 (x>0),由(Ⅰ)知,g(x)在x=e处取得最大值
(x>0),由(Ⅰ)知,g(x)在x=e处取得最大值 .
.
所以 ,即a的取值范围为
,即a的取值范围为 .(13分)
.(13分)
点评:本题主要考查函数、导数、不等式等基础知识,以及综合运用上述知识分析问题和解决问题的能力.
 ,再利用导数与单调性关系解得即可;
,再利用导数与单调性关系解得即可;(2)存在性问题,只需等价于只需
 在(0,+∞)上的最大值小于a即可,函数的最值问题利用导数解决.
在(0,+∞)上的最大值小于a即可,函数的最值问题利用导数解决.解答:解:(Ⅰ)由导数运算法则知,
 .
.令f'(x)=0,得x=em.(3分)
当x∈(0,em)时,f'(x)>0,f(x)单调递增;
当x∈(em,+∞)时,f'(x)<0,f(x)单调递减.
故当x=em时,f(x)有极大值,且极大值为f(em)=e-m.(6分)
(Ⅱ)欲使lnx-ax<0在(0,+∞)上恒成立,只需
 在(0,+∞)上恒成立,
在(0,+∞)上恒成立,等价于只需
 在(0,+∞)上的最大值小于a.(9分)
在(0,+∞)上的最大值小于a.(9分)设
 (x>0),由(Ⅰ)知,g(x)在x=e处取得最大值
(x>0),由(Ⅰ)知,g(x)在x=e处取得最大值 .
.所以
 ,即a的取值范围为
,即a的取值范围为 .(13分)
.(13分)点评:本题主要考查函数、导数、不等式等基础知识,以及综合运用上述知识分析问题和解决问题的能力.

练习册系列答案
相关题目
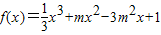 ,m∈R.
,m∈R. ,m∈R.
,m∈R.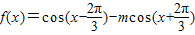 (m∈R)的图象经过点p(0,0)
(m∈R)的图象经过点p(0,0)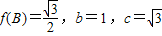 ,且a>b,试判断△ABC的形状,并说明理由.
,且a>b,试判断△ABC的形状,并说明理由.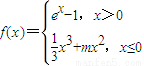 (m∈R,e是自然常数).
(m∈R,e是自然常数).