题目内容
(11分)设集合P={1,2,3}和Q={-1,1,2,3,4},分别从集合P和Q中随机取一个数作为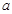 和
和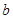 组成数对(
组成数对(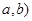 ,并构成函数
,并构成函数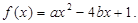
(Ⅰ)写出所有可能的数对(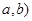 ,并计算
,并计算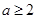 ,且
,且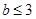 的概率;
的概率;
(Ⅱ)求函数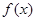 在区间[
在区间[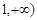 上是增函数的概率.
上是增函数的概率.
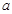 和
和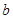 组成数对(
组成数对(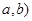 ,并构成函数
,并构成函数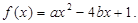
(Ⅰ)写出所有可能的数对(
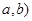 ,并计算
,并计算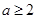 ,且
,且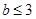 的概率;
的概率;(Ⅱ)求函数
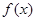 在区间[
在区间[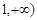 上是增函数的概率.
上是增函数的概率.(Ⅰ)所有基本事件如下:
(1,-1),(1,1),(1,2),(1,3),(1,4),
(2,-1),(2,1),(2,2),(2,3),(2,4),
(3,-1),(3,1),(3,2),(3,3),(3,4),共有15个.P(A)= ;
;
(Ⅱ)P(B)=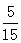 =
=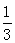 。
。
(1,-1),(1,1),(1,2),(1,3),(1,4),
(2,-1),(2,1),(2,2),(2,3),(2,4),
(3,-1),(3,1),(3,2),(3,3),(3,4),共有15个.P(A)=
 ;
;(Ⅱ)P(B)=
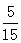 =
=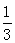 。
。试题分析:(Ⅰ)所有基本事件如下:
(1,-1),(1,1),(1,2),(1,3),(1,4),
(2,-1),(2,1),(2,2),(2,3),(2,4),
(3,-1),(3,1),(3,2),(3,3),(3,4),共有15个. ……2分
设事件“a≥2,且b≤3”为A, ……3分
则事件A包含的基本事件有(2,-1),(2,1),(2,2),(2,3),(3,-1),(3,1),(3,2),(3,3)共8个, ……4分
所以P(A)=
 ……5分
……5分(Ⅱ)设事件“f(x)=ax2-4bx+1在区间[1,+∞)上为增函数”为B,因函数f(x)=ax2-4bx+1的图象的对称轴为x=
 ……7分
……7分且a>0,
所以要使事件B发生,只需
 ≤1即2b≤a. ……9分
≤1即2b≤a. ……9分由满足题意的数对有(1,-1)、(2,-1)、(2,1)、(3,-1)、(3,1),共5个,……10分
∴P(B)=
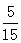 =
=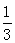 ……11分
……11分点评:综合题,古典概型概率的计算,关键是明确基本事件总数及导致事件发生的基本事件数,根据题中条件,首先得到a,b的关系。

练习册系列答案
相关题目
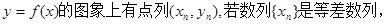 数列{
数列{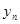 }是等比数列,则函数
}是等比数列,则函数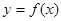 的解析式可能为( )
的解析式可能为( )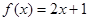
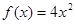
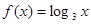
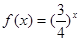
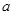 和
和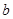 ,定义运算“
,定义运算“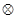 ”:
”: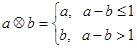 ,设函数
,设函数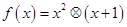 ,若函数
,若函数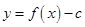 恰有两个不同的零点,则实数
恰有两个不同的零点,则实数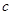 的取值范围是 ( )
的取值范围是 ( ) 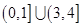
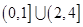
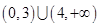
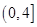
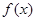 的边际函数
的边际函数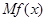 定义为
定义为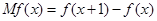 .某公司每月最多生产100台报警系统装置,生产
.某公司每月最多生产100台报警系统装置,生产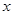 台(
台(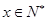 )的收入函数为
)的收入函数为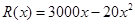 (单位:元),其成本函数为
(单位:元),其成本函数为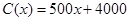 (单位:元),利润是收入与成本之差.
(单位:元),利润是收入与成本之差.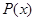 及边际利润函数
及边际利润函数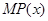 的解析式,并指出它们的定义域;
的解析式,并指出它们的定义域;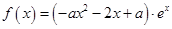 ,
,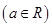
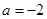 时,求函数
时,求函数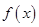 的极值;
的极值;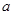 的取值范围.
的取值范围.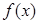 为
为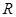 上的减函数,则满足
上的减函数,则满足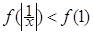 的实数
的实数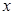 的取值范围是( )
的取值范围是( )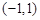
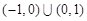
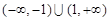
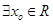 ,使
,使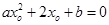 成立,则
成立,则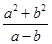 的最小值为( )
的最小值为( )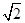
 在区间[0,4]上是增函数, 则
在区间[0,4]上是增函数, 则 和
和 的大小关系是 ( )
的大小关系是 ( )

