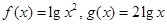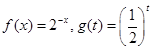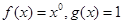题目内容
对实数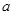 和
和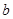 ,定义运算“
,定义运算“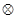 ”:
”: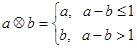 ,设函数
,设函数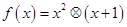 ,若函数
,若函数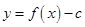 恰有两个不同的零点,则实数
恰有两个不同的零点,则实数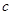 的取值范围是 ( )
的取值范围是 ( )
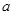 和
和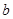 ,定义运算“
,定义运算“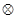 ”:
”: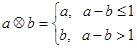 ,设函数
,设函数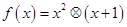 ,若函数
,若函数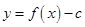 恰有两个不同的零点,则实数
恰有两个不同的零点,则实数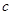 的取值范围是 ( )
的取值范围是 ( ) A.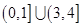 | B.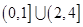 | C.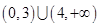 | D.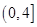 |
A
试题分析:由题意知:
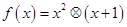
 ,画出函数
,画出函数 的图像,由图像可知;要使函数
的图像,由图像可知;要使函数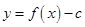 恰有两个不同的零点,
恰有两个不同的零点,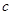 的范围为
的范围为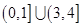 。
。
点评:函数的零点、对应方程的根、函数图像的交点,三者可以转化。本题就是把“函数
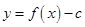 恰有两个不同的零点”转化为“函数
恰有两个不同的零点”转化为“函数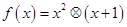
 和函数
和函数 有两个不同的交点”来做的,体现了转化与化规的数学思想,以及数形结合的数学思想。
有两个不同的交点”来做的,体现了转化与化规的数学思想,以及数形结合的数学思想。
练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
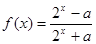 ,若
,若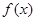 为定义在R上的奇函数,则(1)求实数
为定义在R上的奇函数,则(1)求实数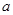 的值;(2)求函数
的值;(2)求函数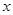 的不等式:
的不等式: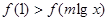
 ,都有
,都有 ,且
,且 ,则
,则 是( )
是( ) 在(0,+∞)上为增函数,且
在(0,+∞)上为增函数,且 ,则不等式
,则不等式 的解集是 .
的解集是 .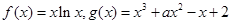
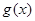 的单调减区间为
的单调减区间为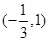 ,求函数
,求函数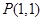 的切线方程;
的切线方程;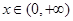 ,不等式
,不等式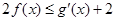 恒成立,求实数
恒成立,求实数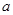 的取值范围。
的取值范围。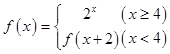 ,则
,则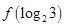 = 。
= 。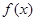
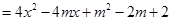 的图像与
的图像与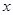 轴有两个交点
轴有两个交点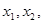 试判断函数
试判断函数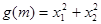 有没有最大值或最小值,并说明理由.
有没有最大值或最小值,并说明理由. 在区间
在区间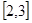 上都是减函数,求实数
上都是减函数,求实数 的取值范围.
的取值范围.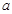 和
和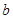 组成数对(
组成数对(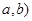 ,并构成函数
,并构成函数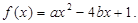
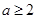 ,且
,且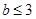 的概率;
的概率;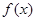 在区间[
在区间[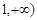 上是增函数的概率.
上是增函数的概率.