题目内容
若ai>0(i=1,2,3,…,n),且a1+a2+…+an=1,证明:a12+a22+…+an2≥
. (n≥2,n∈N)
| 1 |
| n |
由柯西不等式(a1+a2+a2+a3+a3+a4+…+an+a1)×(
+
+…+
)
≥(a1+a2+…+an)2=1.
即2(
+
+…+
)≥(a1+a2+…+an)2=1.
(
+
+…+
)≥
,
令a1=a2=…=a1=
,得a12+a22+…+an2≥
. (n≥2,n∈N).
| a12 |
| a1+a2 |
| a22 |
| a2+a3 |
| an2 |
| an +a1 |
≥(a1+a2+…+an)2=1.
即2(
| a12 |
| a1+a2 |
| a22 |
| a2+a3 |
| an2 |
| an +a1 |
(
| a12 |
| a1+a2 |
| a22 |
| a2+a3 |
| an2 |
| an +a1 |
| 1 |
| 2 |
令a1=a2=…=a1=
| 1 |
| n |
| 1 |
| n |

练习册系列答案
相关题目
 (文科做)已知点A1(2,0),A2(1,t),A3(0,b),A4(-1,t),A5(-2,0),其中t>0,b为正常数.
(文科做)已知点A1(2,0),A2(1,t),A3(0,b),A4(-1,t),A5(-2,0),其中t>0,b为正常数.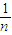 . (n≥2,n∈N)
. (n≥2,n∈N)