题目内容
已知椭圆C: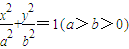 的焦距为
的焦距为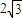 ,离心率为
,离心率为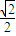 ,其右焦点为F,过点B(0,b)作直线交椭圆于另一点A.
,其右焦点为F,过点B(0,b)作直线交椭圆于另一点A.(Ⅰ)若
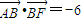 ,求△ABF外接圆的方程;
,求△ABF外接圆的方程;(Ⅱ)若过点M(2,0)的直线与椭圆N:
 相交于两点G、H,设P为N上一点,且满足
相交于两点G、H,设P为N上一点,且满足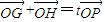 (O为坐标原点),当
(O为坐标原点),当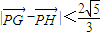 时,求实数t的取值范围.
时,求实数t的取值范围.
【答案】分析:(Ⅰ)利用椭圆的简单性质求得它的标准方程,设A(x,y),由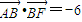 ,求得A的坐标,由此求得三角形外接圆的半径,即可求得外接圆的方程.
,求得A的坐标,由此求得三角形外接圆的半径,即可求得外接圆的方程.
(Ⅱ)由题意可知直线GH的斜率存在,把GH的方程代入椭圆,由判别式大于零求得 (*).再由
(*).再由 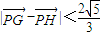 ,求得
,求得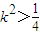 ,结合(*)得
,结合(*)得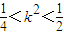 .根据
.根据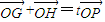 ,即(x1+x2,y1+y2)=t(x,y),结合点P在椭圆上可得16k2=t2(1+2k2),从而求得实数t的取值范围.
,即(x1+x2,y1+y2)=t(x,y),结合点P在椭圆上可得16k2=t2(1+2k2),从而求得实数t的取值范围.
解答:解:(Ⅰ)由题意知: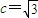 ,
,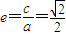 ,又a2-b2=c2,
,又a2-b2=c2,
解得: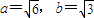 ,∴椭圆C的方程为:
,∴椭圆C的方程为: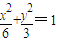 .…(2分)
.…(2分)
可得: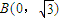 ,
,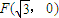 ,设A(x,y),则
,设A(x,y),则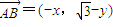 ,
,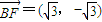 ,
,
∵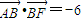 ,∴
,∴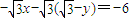 ,即
,即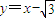 .
.
由
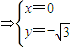 ,或
,或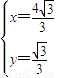 ,
,
即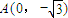 ,或
,或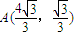 …(4分)
…(4分)
①当A的坐标为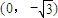 时,
时,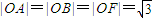 ,
,
∴△ABF外接圆是以O为圆心,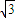 为半径的圆,即x2+y2=3.…(5分)
为半径的圆,即x2+y2=3.…(5分)
②当A的坐标为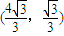 时,kAF=1,kBF=-1,所以△ABF为直角三角形,其外接圆是以线段AB为直径的圆,
时,kAF=1,kBF=-1,所以△ABF为直角三角形,其外接圆是以线段AB为直径的圆,
圆心坐标为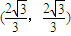 ,半径为
,半径为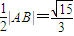 ,
,
∴△ABF外接圆的方程为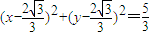 .
.
综上可知:△ABF外接圆方程是x2+y2=3,或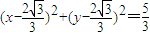 .…(7分)
.…(7分)
(Ⅱ)由以上可得,椭圆N:即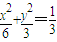 ,即
,即 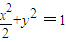 .
.
由题意可知直线GH的斜率存在,设GH:y=k(x-2),G(x1,y1),H(x2,y2),P(x,y),
由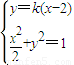 得:(1+2k2)x2-8k2x+8k2-2=0,
得:(1+2k2)x2-8k2x+8k2-2=0,
由△=64k4-4(2k2+1)(8k2-2)>0得: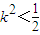 (*). …(9分)
(*). …(9分)
由于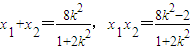 ,∵
,∵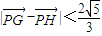 ,
,
∴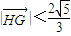 ,即
,即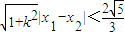 ,∴
,∴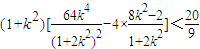 ,
,
∴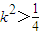 ,再结合(*)得:
,再结合(*)得: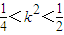 .…(11分)
.…(11分)
∵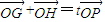 ,∴(x1+x2,y1+y2)=t(x,y)
,∴(x1+x2,y1+y2)=t(x,y)
从而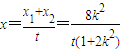 ,
,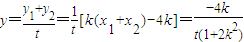 .
.
∵点P在椭圆上,∴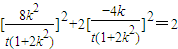 ,整理得:16k2=t2(1+2k2),
,整理得:16k2=t2(1+2k2),
即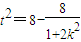 ,∴
,∴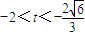 ,或
,或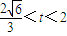 ,
,
即实数t的取值范围为 (-2,- ∪(
∪(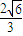 ,2).…(13分)
,2).…(13分)
点评:本题主要考查椭圆的标准方程和简单性质,求圆的标准方程得方法,直线和圆的位置关系,两个向量的数量积的运算,属于中档题.
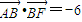 ,求得A的坐标,由此求得三角形外接圆的半径,即可求得外接圆的方程.
,求得A的坐标,由此求得三角形外接圆的半径,即可求得外接圆的方程.(Ⅱ)由题意可知直线GH的斜率存在,把GH的方程代入椭圆,由判别式大于零求得
 (*).再由
(*).再由 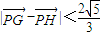 ,求得
,求得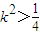 ,结合(*)得
,结合(*)得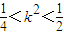 .根据
.根据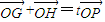 ,即(x1+x2,y1+y2)=t(x,y),结合点P在椭圆上可得16k2=t2(1+2k2),从而求得实数t的取值范围.
,即(x1+x2,y1+y2)=t(x,y),结合点P在椭圆上可得16k2=t2(1+2k2),从而求得实数t的取值范围.解答:解:(Ⅰ)由题意知:
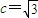 ,
,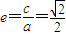 ,又a2-b2=c2,
,又a2-b2=c2,解得:
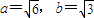 ,∴椭圆C的方程为:
,∴椭圆C的方程为: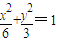 .…(2分)
.…(2分)可得:
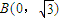 ,
,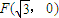 ,设A(x,y),则
,设A(x,y),则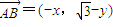 ,
,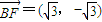 ,
,∵
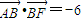 ,∴
,∴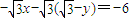 ,即
,即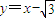 .
.由

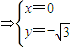 ,或
,或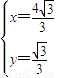 ,
,即
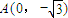 ,或
,或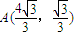 …(4分)
…(4分)①当A的坐标为
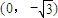 时,
时,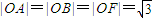 ,
,∴△ABF外接圆是以O为圆心,
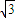 为半径的圆,即x2+y2=3.…(5分)
为半径的圆,即x2+y2=3.…(5分)②当A的坐标为
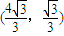 时,kAF=1,kBF=-1,所以△ABF为直角三角形,其外接圆是以线段AB为直径的圆,
时,kAF=1,kBF=-1,所以△ABF为直角三角形,其外接圆是以线段AB为直径的圆,圆心坐标为
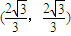 ,半径为
,半径为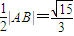 ,
,∴△ABF外接圆的方程为
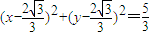 .
.综上可知:△ABF外接圆方程是x2+y2=3,或
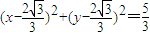 .…(7分)
.…(7分)(Ⅱ)由以上可得,椭圆N:即
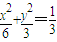 ,即
,即 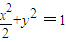 .
.由题意可知直线GH的斜率存在,设GH:y=k(x-2),G(x1,y1),H(x2,y2),P(x,y),
由
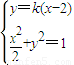 得:(1+2k2)x2-8k2x+8k2-2=0,
得:(1+2k2)x2-8k2x+8k2-2=0,由△=64k4-4(2k2+1)(8k2-2)>0得:
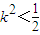 (*). …(9分)
(*). …(9分)由于
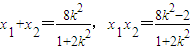 ,∵
,∵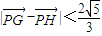 ,
,∴
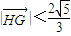 ,即
,即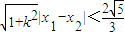 ,∴
,∴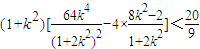 ,
,∴
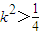 ,再结合(*)得:
,再结合(*)得: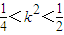 .…(11分)
.…(11分)∵
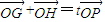 ,∴(x1+x2,y1+y2)=t(x,y)
,∴(x1+x2,y1+y2)=t(x,y)从而
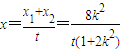 ,
,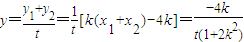 .
.∵点P在椭圆上,∴
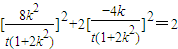 ,整理得:16k2=t2(1+2k2),
,整理得:16k2=t2(1+2k2),即
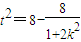 ,∴
,∴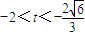 ,或
,或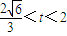 ,
,即实数t的取值范围为 (-2,-
 ∪(
∪(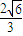 ,2).…(13分)
,2).…(13分)点评:本题主要考查椭圆的标准方程和简单性质,求圆的标准方程得方法,直线和圆的位置关系,两个向量的数量积的运算,属于中档题.

练习册系列答案
相关题目
 已知椭圆D:
已知椭圆D: 的焦距等于
的焦距等于 ,且过点
,且过点

 与椭圆D交于A、B两点,求证:直线NA与直线NB的倾角互补.
与椭圆D交于A、B两点,求证:直线NA与直线NB的倾角互补.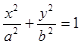
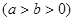 的短轴长等于焦距,椭圆C上的点到右焦点
的短轴长等于焦距,椭圆C上的点到右焦点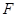 的最短距离为
的最短距离为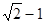 .
.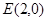 且斜率为
且斜率为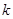 (
(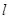 与C交于
与C交于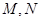 两点,
两点,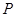 是点
是点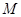 关于
关于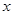 轴的对称点,证明:
轴的对称点,证明: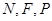 三点共线.
三点共线. 已知椭圆D:
已知椭圆D: 的焦距等于
的焦距等于 ,且过点
,且过点

 与椭圆D交于A、B两点,求证:直线NA与直线NB的倾角互补.
与椭圆D交于A、B两点,求证:直线NA与直线NB的倾角互补. 的焦距为4,且与椭圆
的焦距为4,且与椭圆 有相同的离心率,斜率为k的直线
有相同的离心率,斜率为k的直线 经过点M(0,1),与椭圆C交于不同两点A,B。
经过点M(0,1),与椭圆C交于不同两点A,B。