题目内容
(本小题满分12分)
如图,已知圆C与y轴相切于点T(0,2),与x轴正半轴相交于两点M,N(点M必在点N的右侧),且 已知椭圆D:
已知椭圆D: 的焦距等于
的焦距等于 ,且过点
,且过点

( I ) 求圆C和椭圆D的方程;
(Ⅱ) 若过点M斜率不为零的直线 与椭圆D交于A、B两点,求证:直线NA与直线NB的倾角互补.
与椭圆D交于A、B两点,求证:直线NA与直线NB的倾角互补.
(1) 圆 的方程是
的方程是 ,椭圆
,椭圆 的方程为
的方程为 .
.
(2)利用直线的斜率互为相反数来证明
解析试题分析:解:(Ⅰ)设圆的半径为 ,由题意,圆心为
,由题意,圆心为 ,因为
,因为 ,
,
所以
故圆 的方程是
的方程是 ①
①
在①中,令 解得
解得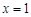 或
或 ,所以
,所以
由 得
得 ,故
,故
所以椭圆 的方程为
的方程为 .
.
(Ⅱ)设直线 的方程为
的方程为
由 得
得

设
则
因为



=0.
所以 ,
,
当 或
或 时,
时, ,此时,对方程
,此时,对方程 ,
, ,不合题意.
,不合题意.
所以直线 与直线
与直线 的倾斜角互补.
的倾斜角互补.
考点:本试题考查了圆和椭圆的方程。
点评:解决该试题的关键是利用待定系数法来和题目中的条件得到关系式,求解得到方程,同时对于直线与椭圆相交时,判定直线的倾斜角互补,只要求解斜率互为相反数即可,属于中档题。

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目