题目内容
(本小题满分14分)已知函数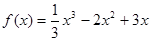 (
(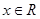 )的图象为曲线
)的图象为曲线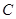 .
.
(Ⅰ)求曲线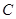 上任意一点处的切线的斜率的取值范围;
上任意一点处的切线的斜率的取值范围;
(Ⅱ)若曲线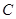 上存在两点处的切线互相垂直,求其中一条切线与曲线
上存在两点处的切线互相垂直,求其中一条切线与曲线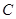 的切点的横坐标的取值范围;
的切点的横坐标的取值范围;
(Ⅲ)试问:是否存在一条直线与曲线C同时切于两个不同点?如果存在,求出符合条件的所有直线方程;若不存在,说明理由.
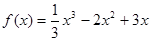 (
(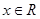 )的图象为曲线
)的图象为曲线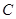 .
.(Ⅰ)求曲线
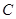 上任意一点处的切线的斜率的取值范围;
上任意一点处的切线的斜率的取值范围;(Ⅱ)若曲线
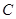 上存在两点处的切线互相垂直,求其中一条切线与曲线
上存在两点处的切线互相垂直,求其中一条切线与曲线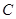 的切点的横坐标的取值范围;
的切点的横坐标的取值范围;(Ⅲ)试问:是否存在一条直线与曲线C同时切于两个不同点?如果存在,求出符合条件的所有直线方程;若不存在,说明理由.
(1) 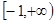 (2)
(2) 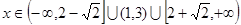 (3) 不存在一条直线与曲线C同时切于两点
(3) 不存在一条直线与曲线C同时切于两点
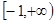 (2)
(2) 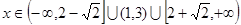 (3) 不存在一条直线与曲线C同时切于两点
(3) 不存在一条直线与曲线C同时切于两点试题分析:解:(Ⅰ)
 ,则
,则 ,
,即曲线
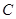 上任意一点处的切线的斜率的取值范围是
上任意一点处的切线的斜率的取值范围是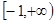 ;------------3分
;------------3分(Ⅱ)由(1)可知,
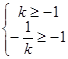 ---------------------------------------------------------5分
---------------------------------------------------------5分解得
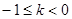 或
或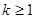 ,由
,由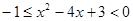 或
或
得:
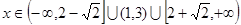 ;-------------------------------7分
;-------------------------------7分(Ⅲ)设存在过点A
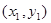 的切线曲线C同时切于两点,另一切点为B
的切线曲线C同时切于两点,另一切点为B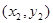 ,
, ,
,则切线方程是:
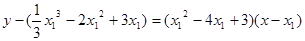 ,
,化简得:
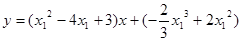 ,
,而过B
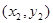 的切线方程是
的切线方程是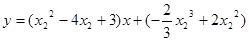 ,
, 由于两切线是同一直线,
则有:
 ,得
,得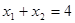 ,----------------------11分
,----------------------11分又由
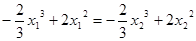 ,
,即
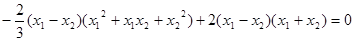
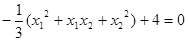 ,即
,即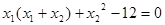
即
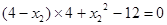 ,
,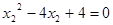
得
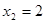 ,但当
,但当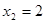 时,由
时,由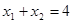 得
得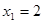 ,这与
,这与 矛盾。
矛盾。所以不存在一条直线与曲线C同时切于两点. ---------------14分
点评:对于切线方程的求解主要抓住两点:第一是切点,第二就是切点出的切线的斜率。然后结合点斜式方程来得到。以及利用函数的思想求解斜率的范围,或者确定方程的解即为切线的条数问题。

练习册系列答案
相关题目
 在
在 处取得极大值
处取得极大值 ,则
,则 的值为 .
的值为 . 在
在 内有极小值,则实数
内有极小值,则实数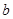 的取值范围
的取值范围 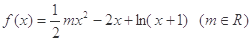 .
.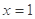 能否为函数
能否为函数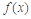 的极值点,并说明理由;
的极值点,并说明理由;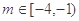 ,使得定义在
,使得定义在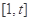 上的函数
上的函数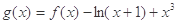 在
在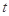 的最大值.
的最大值. 
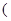
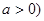 .
.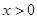 时,求证:
时,求证: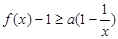 ;
;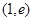 上
上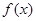
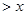 恒成立,求实数
恒成立,求实数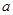 的范围。
的范围。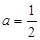 时,求证:
时,求证: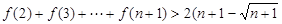 )
)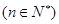 .
.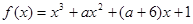 既有极大值又有极小值,则
既有极大值又有极小值,则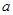 的取值范围为( )
的取值范围为( )



 在
在 及
及 时取得极值.
时取得极值. ,都有
,都有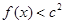 成立,求c的取值范围(6分)
成立,求c的取值范围(6分)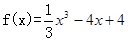 在
在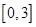 上的最大值是( )
上的最大值是( )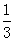
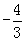
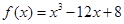 在区间
在区间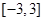 上的最大值与最小值分别为
上的最大值与最小值分别为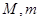 ,则
,则 .
.