Question

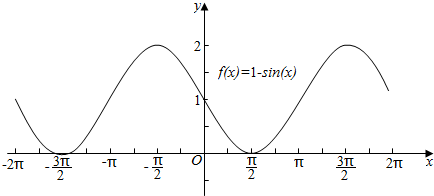
13．用五点法分别作下列函数在[-2π，2π]上的图象：
（1）y=1-sinx；
（2）y=sin（-x）．

Answer 1

分析 （1）利用五点法作出函数y=1-sinx（0≤x≤2π）的简图，再向左边平移图象即可得解．
（2）由条件利用五点法作出函数y=-sinx在[0，2π]上的图象，再向左边平移图象即可得解．

解答 解：（1）解：∵y=1-sinx，周期T=2π，
∴利用五点法作出函数y=1-sinx（0≤x≤2π）的简图，再向左边平移图象即可得解．
列表：

x	0	$\frac{π}{2}$	π	$\frac{3π}{2}$	2π
sinx	0	1	0	-1	0
y=1-sinx	1	0	1	2	1

描点，连线，平移，可得图象如下：


（2）∵y=sin（-x）．周期T=2π，
∴利用五点法作出函数y=1-sinx（0≤x≤2π）的简图，再向左边平移图象即可得解．
列表：

x	0	$\frac{π}{2}$	π	$\frac{3π}{2}$	2π
y	0	-1	0	1	0

描点，连线，平移，可得图象如下：

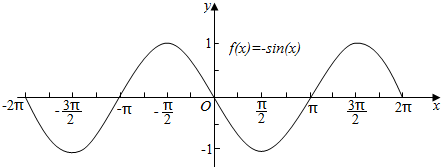
点评 本题主要考查用五点法作函数y=Asin（ωx+φ）在一个周期上的图象，属于基础题．