题目内容
18.若方程x+y-4$\sqrt{x+y}$+2k=0表示两条不同直线,则k的取值范围是( )| A. | k<2 | B. | k≤2 | C. | .0≤k<2 | D. | 0≤k≤2 |
分析 令$\sqrt{x+y}=t$(t≥0),把原方程化为t2-4t+2k=0,由题意可得$\left\{\begin{array}{l}{△=16-8k>0}\\{2k≥0}\end{array}\right.$,求解不等式组得答案.
解答 解:令$\sqrt{x+y}=t$(t≥0),
则方程x+y-4$\sqrt{x+y}$+2k=0化为t2-4t+2k=0,
要使方程x+y-4$\sqrt{x+y}$+2k=0表示两条不同直线,
则方程t2-4t+2k=0有两不等非负根,
即$\left\{\begin{array}{l}{△=16-8k>0}\\{2k≥0}\end{array}\right.$,解得:0≤k<2.
故选:C.
点评 本题考查曲线与方程,训练了一元二次方程根与系数关系的应用,考查了数学转化思想方法,是中档题.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
6.已知sinx•$\sqrt{si{n}^{2}x}$+cosx•$\sqrt{co{s}^{2}x}$=-1,则x为( )
| A. | 第一象限的角 | B. | 第二象限的角 | C. | 第三象限的角 | D. | 第四象限的角 |
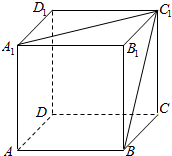 在正方体ABCD-A1B1C1D1中,求:
在正方体ABCD-A1B1C1D1中,求: