题目内容
【题目】已知椭圆 
的离心率为 
，其左顶点A在圆O：x2+y2=16上． 
（1）求椭圆W的方程；
（2）若点P为椭圆W上不同于点A的点，直线AP与圆O的另一个交点为Q．是否存在点P，使得 
？若存在，求出点P的坐标；若不存在，说明理由．
【答案】
（1）解：因为椭圆W的左顶点A在圆O：x2+y2=16上，
令y=0，得x=±4，所以a=4．
又离心率为 
，所以 
，所以 
，
所以b2=a2﹣c2=4，
所以W的方程为 
．
（2）解：
法一：设点P（x1，y1），Q（x2，y2），设直线AP的方程为y=k（x+4），
与椭圆方程联立得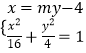 
，
化简得到（1+4k2）x2+32k2x+64k2﹣16=0
因为﹣4为上面方程的一个根，所以 
，所以 
．
所以 
．
因为圆心到直线AP的距离为 
，
所以 
，
因为 
，
代入得到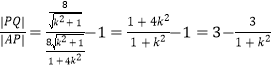 
．
显然 
，所以不存在直线AP，使得 
．
法二：
设点P（x1，y1），Q（x2，y2），设直线AP的方程为x=my﹣4，
与椭圆方程联立得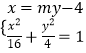
化简得到（m2+4）y2﹣8my=0，由△=64m2＞0得m≠0．
显然0是上面方程的一个根，所以另一个根，即 
．
由 
因为圆心到直线AP的距离为 ，
所以 
．
因为 ，
代入得到 
，
若 
，则m=0，与m≠0矛盾，矛盾，
所以不存在直线AP，使得 ．
法三：假设存在点P，使得 ，则 
，得 
．
显然直线AP的斜率不为零，设直线AP的方程为x=my﹣4，
由 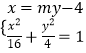，得（m2+4）y2﹣8my=0，
由△=64m2＞0得m≠0，
所以 
．
同理可得 
，
所以由 得 
，
则m=0，与m≠0矛盾，
所以不存在直线AP，使得
【解析】（1）由题意求出a，通过离心率求出c，然后求解椭圆的标准方程．（2）法一：设点P（x1 ， y1），Q（x2 ， y2），设直线AP的方程为y=k（x+4），与椭圆方程联立，利用弦长公式求出|AP|，利用垂径定理求出|oa|，即可得到结果．
法二：设点P（x1 ， y1），Q（x2 ， y2），设直线AP的方程为x=my﹣4，与椭圆方程联立与椭圆方程联立得求出|AP|，利用垂径定理求出|oa|，即可得到结果．
法三：假设存在点P，推出 ，设直线AP的方程为x=my﹣4，联立直线与椭圆的方程，利用韦达定理，推出 ，求解即可．
【考点精析】本题主要考查了椭圆的标准方程的相关知识点，需要掌握椭圆标准方程焦点在x轴：
，焦点在y轴：
才能正确解答此题．
