题目内容
已知:直线x+y=1交椭圆mx2+ny2=1于A,B两点,且OA⊥OB(O为坐标原点)(1)求证:椭圆过定点;
(2)若椭圆的离心率在[
| ||
| 3 |
| ||
| 2 |
分析:(1)由
?(m+n)x2-2nx+n-1=0,由△=4n2-4(m+n)(n-1)>0得:m+n-mn>0,设A(x1,y1),B(x2,y2),则:x1+x2=
,x1x2=
,由此能够推导出椭圆恒过定点.
(2)设椭圆的焦点在x轴上,由
≤e≤
,知
≤e2≤
,所以
≤
≤
.由n=2-m,得
≤
≤
,得
≤
≤
,由此能求出椭圆长轴的取值范围.
|
| 2n |
| m+n |
| n-1 |
| m+n |
(2)设椭圆的焦点在x轴上,由
| ||
| 3 |
| ||
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| m |
| n |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 | ||
|
| 2 |
| 3 |
| ||
| 2 |
|
| ||
| 2 |
解答:解:(1)证明:由
?(m+n)x2-2nx+n-1=0…(2分)
由△=4n2-4(m+n)(n-1)>0得:m+n-mn>0
设A(x1,y1),B(x2,y2),则:x1+x2=
,x1x2=
∵OA⊥OB,∴x1x2+(1-x1)(1-x2)=0,即2x1x2-(x1+x2)+1=0,
得
-
+1=0,即
m+
n=1.
∴椭圆恒过定点(
,
),(
,-
),(-
,
),(-
,-
).
(2)设椭圆的焦点在x轴上,
∵
≤e≤
,∴
≤e2≤
,∴
≤
≤
.
由(1)得n=2-m,代入上式,得
≤
≤
,得
≤
≤
,
∴
≤2
≤
,
∴椭圆长轴的取值范围是[
,
].
|
由△=4n2-4(m+n)(n-1)>0得:m+n-mn>0
设A(x1,y1),B(x2,y2),则:x1+x2=
| 2n |
| m+n |
| n-1 |
| m+n |
∵OA⊥OB,∴x1x2+(1-x1)(1-x2)=0,即2x1x2-(x1+x2)+1=0,
得
| 2(n-1) |
| m+n |
| 2n |
| m+n |
| 1 |
| 2 |
| 1 |
| 2 |
∴椭圆恒过定点(
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
(2)设椭圆的焦点在x轴上,
∵
| ||
| 3 |
| ||
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| m |
| n |
| 2 |
| 3 |
由(1)得n=2-m,代入上式,得
| 1 |
| 2 |
| 1 | ||
|
| 2 |
| 3 |
| ||
| 2 |
|
| ||
| 2 |
∴
| 5 |
|
| 6 |
∴椭圆长轴的取值范围是[
| 5 |
| 6 |
点评:本题考查椭圆过定点的证明和求椭圆长轴的取值范围.解题时要认真审题,注意椭圆性质的灵活运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
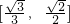 上变化时,求椭圆长轴的取值范围.
上变化时,求椭圆长轴的取值范围.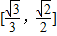 上变化时,求椭圆长轴的取值范围.
上变化时,求椭圆长轴的取值范围.