题目内容

已知曲线C：(5－m)x2＋(m－2)y2＝8(m∈R)

(1)若曲线C是焦点在x轴上的椭圆，求m的取值范围；

(2)设m＝4，曲线C与y轴的交点为A，B(点A位于点B的上方)，直线y＝kx＋4与曲线C交于不同的两点M，N，直线y＝1与直线BM交于点G．求证：A，G，N三点共线．

答案：
解析：

　　(1)原曲线方程可化简得：

　　由题意可得：，解得：

　　(2)由已知直线代入椭圆方程化简得：，

　　，解得：

　　由韦达定理得：①，，②

　　设，，

　　方程为：，则，

　　，，

　　欲证三点共线，只需证，共线

　　即成立，化简得：

　　将①②代入易知等式成立，则三点共线得证．


练习册系列答案
相关题目
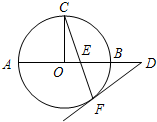精英家教网A（选修4-1：几何证明选讲）
如图，AB是⊙O的直径，C，F是⊙O上的两点，OC⊥AB，过点F作⊙O的切线FD交AB的延长线于点D，连接CF交AB于点E．
求证：DE2=DB•DA．
B（选修4-2：矩阵与变换）
求矩阵
21
12
的特征值及对应的特征向量．
C（选修4-4：坐标系与参数方程）
已知曲线C的极坐标方程是ρ=2sinθ，直线l的参数方程是
x=-
3
5
t+2
y=
4
5
t
（t为参数）．
（Ⅰ）将曲线C的极坐标方程化为直角坐标方程；
（Ⅱ）设直线l与x轴的交点是M，N是曲线C上一动点，求MN的最大值．
D（选修4-5：不等式选讲）
已知m＞0，a，b∈R，求证：(
a+mb
1+m
)2≤
a2+mb2
1+m
．
已知曲线C：（5-2m）x2+（m2+2）y2=4-m2，（m∈R）表示圆，则圆的半径为（　　）
已知曲线C：（5-m）x2+（m-2）y2=8（m∈R），O为坐标原点．
（Ⅰ）若曲线C是焦点在x轴点上的椭圆且离心率e＞
2
2
，求m的取值范围；
（Ⅱ）设m=4，直线l过点（0，1）且与曲线C交于不同的两点A、B，求当△ABO的面积取得最大值时直线l的方程．
[选做题]在下面A，B，C，D四个小题中只能选做两题，每小题10分，共20分．
A．选修4-1：几何证明选讲
如图，⊙O是等腰三角形ABC的外接圆，AB=AC，延长BC到点D，使CD=AC，连接AD交⊙O于点E，连接BE与AC交于点F，判断BE是否平分∠ABC，并说明理由．
B．选修4-2：短阵与变换
已知矩阵M=
1
2
0
02
，矩阵M对应的变换把曲线y=sinx变为曲线C，求C的方程．
C．选修4-4：坐标系与参数方程
已知曲线C的极坐标方程是ρ=4sin(θ+
π
4
)，求曲线C的普通方程．
D．选修4-5：不等式选讲
已知x，y，z∈R，且x+y+z=3，求x2+y2+z2的最小值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网