题目内容
已知曲线C：（5-2m）x2+（m2+2）y2=4-m2，（m∈R）表示圆，则圆的半径为（ ）
分析：由x2和y2项的系数相等求出m的值，因为m2+2＞0，所以求得的m值应满足4-m2＞0，代入m值后整理圆的方程得到圆的半径．
解答：解：由曲线C：（5-2m）x2+（m2+2）y2=4-m2，（m∈R）表示圆，
则5-2m=m2+2＞0，解得：m=-3或m=1．
当m=-3时，4-m2=4-（-3）2=-5＜0不和题意舍去．
∴m=1．
此时圆的方程化为x2+y2=1．
∴圆的半径为1．
故选：B．
则5-2m=m2+2＞0，解得：m=-3或m=1．
当m=-3时，4-m2=4-（-3）2=-5＜0不和题意舍去．
∴m=1．
此时圆的方程化为x2+y2=1．
∴圆的半径为1．
故选：B．
点评：本题考查了圆的标准方程，考查了二元二次方程表示圆的条件，属中档题型．
练习册系列答案
学练快车道快乐假期寒假作业系列答案
新思维寒假作业系列答案
相关题目
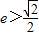，求m的取值范围；