题目内容
已知曲线C:(5-m)x2+(m-2)y2=8(m∈R),O为坐标原点.
(Ⅰ)若曲线C是焦点在x轴点上的椭圆且离心率e>
,求m的取值范围;
(Ⅱ)设m=4,直线l过点(0,1)且与曲线C交于不同的两点A、B,求当△ABO的面积取得最大值时直线l的方程.
(Ⅰ)若曲线C是焦点在x轴点上的椭圆且离心率e>
| ||
| 2 |
(Ⅱ)设m=4,直线l过点(0,1)且与曲线C交于不同的两点A、B,求当△ABO的面积取得最大值时直线l的方程.
分析:(I)先化简方程,根据椭圆的标准方程及离心率不等式求出m满足的条件,再求解.
(II)设出直线方程,及直线与椭圆的交点坐标,再根据弦长公式及三角形面积公式,将面积S表示成K的函数,用换元法求函数S(K)的最值及取的最值的K值.
(II)设出直线方程,及直线与椭圆的交点坐标,再根据弦长公式及三角形面积公式,将面积S表示成K的函数,用换元法求函数S(K)的最值及取的最值的K值.
解答:解:(I)方程化为
+
=1,∵是焦点在x轴点上的椭圆,
∴m-2>5-m>0⇒
<m<5
∵e=
>
⇒4c2>2a2⇒a2>2b2⇒m>4,
∴m的取值范围是4<m<5.
(II)当m=4时,曲线C的方程为:
+
=1,
①当倾斜角为
时,三角形不存在;
②当斜率存在时,设直线方程为y=kx+1,则原点O到直线的距离d=
,
设A(x1,y1),B(x2,y2)为直线与椭圆的两个交点,
联立直线和椭圆方程
消去y可得(2k2+1)x2+4kx-6=0,
则x1+x2=
,x1x2=
,|AB|=
S=
d|AB|=
=
=
=
令t=
,t∈(0,1];
S=
=
=
-
=-2t2+8t=8-2(t-2)2,
在(0,1]单调递增,
∴当t=1时上式为最大值,最大值是6,此时k=0,直线方程为y=1.
| x2 | ||
|
| y2 | ||
|
∴m-2>5-m>0⇒
| 7 |
| 2 |
∵e=
| c |
| a |
| ||
| 2 |
∴m的取值范围是4<m<5.
(II)当m=4时,曲线C的方程为:
| x2 |
| 8 |
| y2 |
| 4 |
①当倾斜角为
| π |
| 2 |
②当斜率存在时,设直线方程为y=kx+1,则原点O到直线的距离d=
| 1 | ||
|
设A(x1,y1),B(x2,y2)为直线与椭圆的两个交点,
联立直线和椭圆方程
|
则x1+x2=
| -4k |
| 1+k2 |
| -6 |
| 1+2k2 |
(1+k2)[(
|
S=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 | ||
|
(1+k2)[(
|
=
| 1 |
| 2 |
(
|
|
|
令t=
| 1 |
| 1+2k2 |
S=
| 16k2+6 |
| (1+2k2)2 |
| 16k2+8-2 |
| (1+2k2)2 |
| 8 |
| 1+2k2 |
| 2 |
| (1+2k2)2 |
在(0,1]单调递增,
∴当t=1时上式为最大值,最大值是6,此时k=0,直线方程为y=1.
点评:本题考查椭圆的标准方程、几何性质及直线与圆锥曲线的最值问题.利用函数思想,构造函数求最值是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
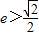 ,求m的取值范围;
,求m的取值范围;