题目内容
设 的三边长分别为
的三边长分别为 ,
, 的面积为
的面积为 ,内切圆半径为
,内切圆半径为 ,则
,则 ;类比这个结论可知:四面体
;类比这个结论可知:四面体 的四个面的面积分别为
的四个面的面积分别为 ,内切球的半径为
,内切球的半径为 ,四面体
,四面体 的体积为
的体积为 ,则
,则 .
.
 的三边长分别为
的三边长分别为 ,
, 的面积为
的面积为 ,内切圆半径为
,内切圆半径为 ,则
,则 ;类比这个结论可知:四面体
;类比这个结论可知:四面体 的四个面的面积分别为
的四个面的面积分别为 ,内切球的半径为
,内切球的半径为 ,四面体
,四面体 的体积为
的体积为 ,则
,则 .
.
试题分析:三角形中,内切圆的圆心,与其三个顶点的连线,构成了三个小的三角形,并且有相同的高
 ,底边分别是
,底边分别是 ,利用等面积法,我们得到
,利用等面积法,我们得到 ,所以
,所以 ;利用类比推理可知,在四面体内切球半径为
;利用类比推理可知,在四面体内切球半径为 ,四个面的面积分别为
,四个面的面积分别为 ,内切球的球心与各顶点的连线,将一个四面体分割为四个小的四面体,以四面体的四个面为底面,高都为
,内切球的球心与各顶点的连线,将一个四面体分割为四个小的四面体,以四面体的四个面为底面,高都为 的四面体,由等体积法,可得到
的四面体,由等体积法,可得到 ,所以
,所以 .
.
练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
 在
在 上是偶函数”的推理过程是( )
上是偶函数”的推理过程是( )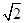 =c+d
=c+d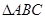 △ABC中,
△ABC中,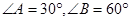 ,求证:
,求证: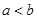 .证明:
.证明: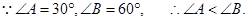 ∴
∴ ,那么
,那么 .
. ,因为对一切实数x,恒有
,因为对一切实数x,恒有 ,所以
,所以  ,从而得
,从而得 ,所以
,所以 时,你能得到的结论为 .(不必证明)
时,你能得到的结论为 .(不必证明)
 ,
, (其中
(其中 ), 则
), 则 ,
, ,根据上面的结论,可以提出猜想: z1·z2·z3= .
,根据上面的结论,可以提出猜想: z1·z2·z3= .