题目内容
已知函数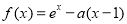 ,其中
,其中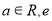 为自然对数底数.
为自然对数底数.
(1)当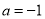 时,求函数
时,求函数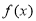 在点
在点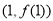 处的切线方程;
处的切线方程;
(2)讨论函数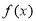 的单调性,并写出相应的单调区间;
的单调性,并写出相应的单调区间;
(3)已知 ,若函数
,若函数 对任意
对任意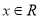 都成立,求
都成立,求 的最大值.
的最大值.
(1)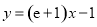 (2)当
(2)当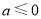 时,函数
时,函数 的单调递增区间为
的单调递增区间为 ;当
;当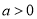 时,函数
时,函数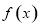 的单调递增区间为
的单调递增区间为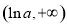 ,单调递减区间为
,单调递减区间为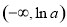 .(3)
.(3)
【解析】
试题分析:(1)根据导数几何意义可求切线斜率: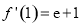 ,再根据点斜式求切线方程为
,再根据点斜式求切线方程为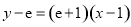 ,即
,即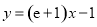 .(2)利用导数求函数单调性,从导函数出发,研究其零点情况:
.(2)利用导数求函数单调性,从导函数出发,研究其零点情况: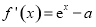 当
当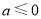 时,
时,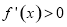 ,无零点,函数
,无零点,函数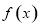 在
在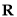 上单调递增;当
上单调递增;当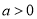 时,由
时,由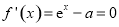 得
得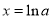 ,
,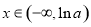 时,
时,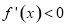 ,
,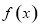 单调递减;
单调递减; 时,
时,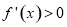 ,
,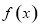 单调递增.(3)不等式恒成立问题转化为函数最值问题:
单调递增.(3)不等式恒成立问题转化为函数最值问题: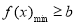 ,当
,当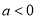 时,函数
时,函数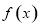 无最小值;当
无最小值;当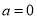 时,函数
时,函数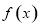 最小值为0,
最小值为0,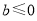 ,此时
,此时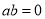 ;当
;当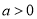 时,
时,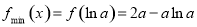 ,
,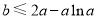 ,
,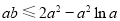 ,最后研究函数
,最后研究函数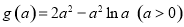 最大值
最大值
试题解析:【解析】
(1)当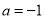 时,
时,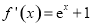 ,
,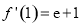 ,
, , 2分
, 2分
∴函数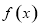 在点
在点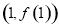 处的切线方程为
处的切线方程为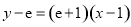 ,
,
即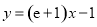 . 4分
. 4分
(2)∵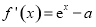 ,
,
①当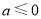 时,
时,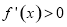 ,函数
,函数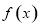 在
在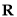 上单调递增; 6分
上单调递增; 6分
②当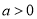 时,由
时,由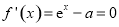 得
得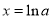 ,
,
∴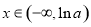 时,
时,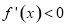 ,
,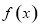 单调递减;
单调递减; 时,
时,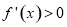 ,
,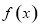 单调递增.
单调递增.
综上,当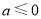 时,函数
时,函数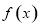 的单调递增区间为
的单调递增区间为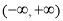 ;当
;当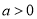 时,函数
时,函数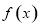 的单调递增区间为
的单调递增区间为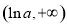 ,单调递减区间为
,单调递减区间为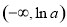 . 9分
. 9分
(3)由(2)知,当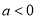 时,函数
时,函数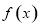 在
在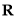 上单调递增,
上单调递增,
∴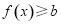 不可能恒成立; 10分
不可能恒成立; 10分
当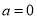 时,
时,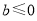 ,此时
,此时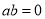 ; 11分
; 11分
当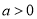 时,由函数
时,由函数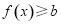 对任意
对任意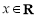 都成立,得
都成立,得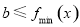 ,
,
∵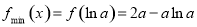 ,∴
,∴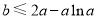 13分
13分
∴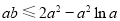 ,
,
设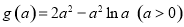 ,∴
,∴ 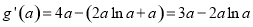 ,
,
由于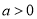 ,令
,令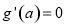 ,得
,得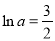 ,
,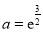 ,
,
当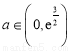 时,
时,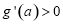 ,
,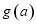 单调递增;
单调递增; 时,
时,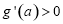 ,
,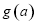 单调递减.
单调递减.
∴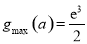 ,即
,即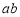 的最大值为
的最大值为 ,
,
此时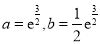 . 16分
. 16分
考点:导数几何意义,利用导数求函数单调性,利用导数求函数最值
考点分析: 考点1:导数及其应用 试题属性- 题型:
- 难度:
- 考核:
- 年级:

(本小题12分)据报道,全国很多省市将英语考试作为高考改革的重点,一时间“英语考试该如何改革”引起广泛关注,为了解某地区学生和包括老师、家长在内的社会人士对高考英语改革的看法,某媒体在该地区选择了3600人进行调查,就“是否取消英语听力”问题进行了问卷调查统计,结果如下表:
态度 调查人群 | 应该取消 | 应该保留 | 无所谓 |
在校学生 | 2100人 | 120人 |
|
社会人士 | 600人 |
|
|
已知在全体样本中随机抽取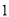 人,抽到持“应该保留”态度的人的概率为
人,抽到持“应该保留”态度的人的概率为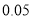
(1)现用分层抽样的方法在所有参与调查的人中抽取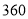 人进行问卷访谈,问应在持“无所谓”态度的人中抽取多少人?
人进行问卷访谈,问应在持“无所谓”态度的人中抽取多少人?
(2)已知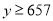 ,
, ,若所选择的在校学生的人数低于被调查人群总数的80%,则认为本次调查“失效”,求本次调查“失效”的概率.
,若所选择的在校学生的人数低于被调查人群总数的80%,则认为本次调查“失效”,求本次调查“失效”的概率.
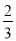 ,命中一次得3分;命中乙靶的概率为
,命中一次得3分;命中乙靶的概率为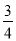 ,命中一次得2分,若没有命中则得0分,用随机变量
,命中一次得2分,若没有命中则得0分,用随机变量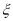 表示该射手一次测试累计得分,如果
表示该射手一次测试累计得分,如果 的最小正周期为 .
的最小正周期为 .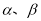 是两个相交平面,则在下列命题中,真命题的序号为 .(写出所有真命题的序号)
是两个相交平面,则在下列命题中,真命题的序号为 .(写出所有真命题的序号) 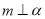 ,则在平面
,则在平面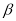 内,一定不存在与直线
内,一定不存在与直线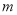 平行的直线.
平行的直线.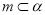 ,则在平面
,则在平面 的定义域为 .
的定义域为 . 为正实数,且
为正实数,且 ,则
,则 的最小值为 .
的最小值为 . 的焦点为顶点,顶点为中心,离心率为2的双曲线标准方程为 .
的焦点为顶点,顶点为中心,离心率为2的双曲线标准方程为 .
 ,则函数
,则函数 的值域为 .
的值域为 . 人
人 人
人 人
人