题目内容
18.在△ABC中,三边长分别为7,$4\sqrt{3}$,$\sqrt{13}$,则三角形最小角的大小为$\frac{π}{6}$.分析 最小的边长度为$\sqrt{13}$,所对的角为θ,θ∈(0,π).利用余弦定理即可得出.
解答 解:最小的边长度为$\sqrt{13}$,所对的角为θ,θ∈(0,π).
$cosθ=\frac{49+48-13}{{2×7×4\sqrt{3}}}=\frac{{\sqrt{3}}}{2}$,
$θ=\frac{π}{6}$.
故答案为:$\frac{π}{6}$.
点评 本题考查了余弦定理,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
9.某校高三子啊一次模拟考试后,为了解数学成绩是否与班级有关,对甲乙两个班数学成绩(满分150分)进行分析,按照不小于120分为优秀,120分以下为非优秀的标准统计成绩,已知从全班100人中随机抽取1人数学成绩优秀的概率为$\frac{3}{10}$,调查结果如表所示.
(1)请完成上面的列联表;
(2)根据列联表的数据,问是否有95%的把握认为“数学成绩与班级有关系”;
(3)若按下面的方法从甲班数学成绩优秀的学生中抽取1人:把甲班数学成绩优秀的10名学生从2到11进行编号,先后两次抛掷一枚均匀的骰子,出现的点数和被记为抽取人的编号,求抽到的编号为6或10的概率.
附:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
| 优秀 | 非优秀 | 总计 | |
| 甲班 | 10 | ||
| 乙班 | 30 | ||
| 合计 | 100 |
(2)根据列联表的数据,问是否有95%的把握认为“数学成绩与班级有关系”;
(3)若按下面的方法从甲班数学成绩优秀的学生中抽取1人:把甲班数学成绩优秀的10名学生从2到11进行编号,先后两次抛掷一枚均匀的骰子,出现的点数和被记为抽取人的编号,求抽到的编号为6或10的概率.
附:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
| P(K2≥k) | 0.05 | 0.01 |
| k | 3.841 | 6.635 |
6.已知函数f(x)=-x5-x3-5x+2,若f(a2)+f(a-2)>4,则实数a的取值范围( )
| A. | (-∞,1) | B. | (-∞,3) | C. | (-2,1) | D. | (-1,2) |
10. 如图是一个四面体的三视图,三个正方形的边长均为2,则四面体外接球的体积为( )
如图是一个四面体的三视图,三个正方形的边长均为2,则四面体外接球的体积为( )
 如图是一个四面体的三视图,三个正方形的边长均为2,则四面体外接球的体积为( )
如图是一个四面体的三视图,三个正方形的边长均为2,则四面体外接球的体积为( )| A. | $\frac{\sqrt{3}}{2}π$ | B. | 4$\sqrt{3}$π | C. | $\frac{4\sqrt{3}}{3}$π | D. | 8$\sqrt{3}$π |
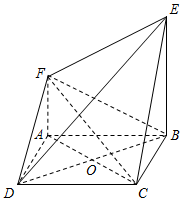 如图,四边形ABCD是正方形,平面ABCD⊥平面ABEF,AF∥BE,AB⊥BE,AB=BE=2,AF=1.
如图,四边形ABCD是正方形,平面ABCD⊥平面ABEF,AF∥BE,AB⊥BE,AB=BE=2,AF=1.