题目内容
定义 ,
,
(Ⅰ)令函数 ,过坐标原点O作曲线C:
,过坐标原点O作曲线C: 的切线
的切线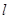 ,切点为P
,切点为P (n>0),设曲线C与
(n>0),设曲线C与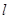 及y轴围成图形的面积为S,求S的值。
及y轴围成图形的面积为S,求S的值。
(Ⅱ)令函数 ,讨论函数
,讨论函数 是否有极值,如果有,说明是极大值还是极小值。
是否有极值,如果有,说明是极大值还是极小值。
(Ⅲ)证明:当
 ,
,(Ⅰ)令函数
 ,过坐标原点O作曲线C:
,过坐标原点O作曲线C: 的切线
的切线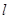 ,切点为P
,切点为P (n>0),设曲线C与
(n>0),设曲线C与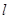 及y轴围成图形的面积为S,求S的值。
及y轴围成图形的面积为S,求S的值。(Ⅱ)令函数
 ,讨论函数
,讨论函数 是否有极值,如果有,说明是极大值还是极小值。
是否有极值,如果有,说明是极大值还是极小值。(Ⅲ)证明:当

(Ⅰ) (Ⅱ)(Ⅲ)当
(Ⅱ)(Ⅲ)当 时,
时, 有极小值,
有极小值, 没有极大值(Ⅲ)见解析
没有极大值(Ⅲ)见解析
 (Ⅱ)(Ⅲ)当
(Ⅱ)(Ⅲ)当 时,
时, 有极小值,
有极小值, 没有极大值(Ⅲ)见解析
没有极大值(Ⅲ)见解析本试题主要是考查了导数在研究函数中的运用,以及定积分的综合运用。
(1)
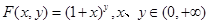 ,
,
 ,
,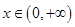 ,
,
曲线C与y轴交点为A(0,1)
又过坐标原点O向曲线C作切线,切点为P(n,t)(n>0),
 ,切线
,切线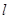 方程为
方程为
(2) ,
,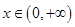 。
。
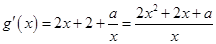 ,
,
那么对于参数a分类讨论得到单调性得到极值。
(3)令
又令

两次构造函数结合导数得到结论。解:(Ⅰ)
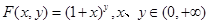 ,
,
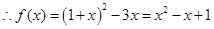 ,
,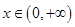 ,
,
曲线C与y轴交点为A(0,1)……………1分
又过坐标原点O向曲线C作切线,切点为P(n,t)(n>0),
 ,切线
,切线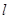 方程为
方程为 …………3分
…………3分
 ………………5分
………………5分
(Ⅱ) ,
,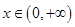 。
。
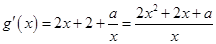 ………………6分
………………6分
1)。当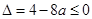 即
即 时,
时, (
(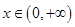 ),
),
 在
在 单调递增从而没有极值; ………………7分
单调递增从而没有极值; ………………7分
2)。当 即
即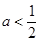 时,方程
时,方程 有二个不等实根
有二个不等实根
 ,
, ,
,
若 ,则
,则 ,
, ,
,
 在
在 单调递增从而没有极值; ………………8分
单调递增从而没有极值; ………………8分
若 ,则
,则 。当
。当 ;当
;当
 当
当 时,
时, 有极小值,
有极小值, 没有极大值。 ………………9分
没有极大值。 ………………9分
(Ⅲ)令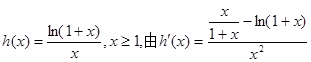 ,…………10分
,…………10分
又令
 ,
,
 单调递减.……………………11分
单调递减.……………………11分
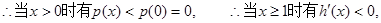
 单调递减,………………12分
单调递减,………………12分
 ,
,
 ………………14分
………………14分
(1)

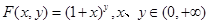 ,
, ,
,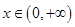 ,
,曲线C与y轴交点为A(0,1)
又过坐标原点O向曲线C作切线,切点为P(n,t)(n>0),

 ,切线
,切线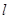 方程为
方程为
(2)
 ,
,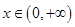 。
。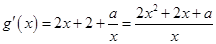 ,
,那么对于参数a分类讨论得到单调性得到极值。
(3)令

又令


两次构造函数结合导数得到结论。解:(Ⅰ)

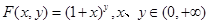 ,
,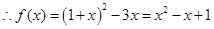 ,
,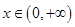 ,
,曲线C与y轴交点为A(0,1)……………1分
又过坐标原点O向曲线C作切线,切点为P(n,t)(n>0),

 ,切线
,切线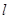 方程为
方程为 …………3分
…………3分 ………………5分
………………5分(Ⅱ)
 ,
,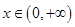 。
。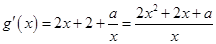 ………………6分
………………6分1)。当
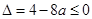 即
即 时,
时, (
(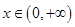 ),
), 在
在 单调递增从而没有极值; ………………7分
单调递增从而没有极值; ………………7分2)。当
 即
即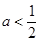 时,方程
时,方程 有二个不等实根
有二个不等实根 ,
, ,
,
若
 ,则
,则 ,
, ,
, 在
在 单调递增从而没有极值; ………………8分
单调递增从而没有极值; ………………8分若
 ,则
,则 。当
。当 ;当
;当
 当
当 时,
时, 有极小值,
有极小值, 没有极大值。 ………………9分
没有极大值。 ………………9分(Ⅲ)令
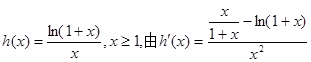 ,…………10分
,…………10分又令

 ,
, 单调递减.……………………11分
单调递减.……………………11分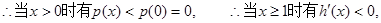
 单调递减,………………12分
单调递减,………………12分 ,
, ………………14分
………………14分
练习册系列答案
相关题目
 )>
)> .若S1=
.若S1= ,S2=
,S2= (b-a),S3=f(a)(b-a),则S1、S2、S3的大小关系为__________.
(b-a),S3=f(a)(b-a),则S1、S2、S3的大小关系为__________. 。
。 的图象上有一点
的图象上有一点 ,此函数图象与
,此函数图象与 轴及直线
轴及直线 围成图形(如图阴影部分)的面积为
围成图形(如图阴影部分)的面积为 ,则
,则 的函数关系
的函数关系 的图象可以是( )
的图象可以是( )

 和
和 所表示的曲线围成的面积为( )
所表示的曲线围成的面积为( )



 ,质点作直线运动,则此物体在时间
,质点作直线运动,则此物体在时间 内的位移为( )
内的位移为( )





 ,
, 所围成图形的面积
所围成图形的面积

 dx等于
dx等于