题目内容
已知函数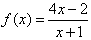
（x≠-1，x∈R），数列{an}满足a1=a（a≠-1，x∈R），an+1=f（an）（n∈N*），
（1）若数列{an}是常数列，求a的值；
（2）当a1=4时，记bn=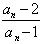
（n∈N*），证明数列{bn}是等比数列，并求
。
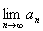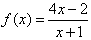（x≠-1，x∈R），数列{an}满足a1=a（a≠-1，x∈R），an+1=f（an）（n∈N*），（1）若数列{an}是常数列，求a的值；
（2）当a1=4时，记bn=
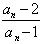（n∈N*），证明数列{bn}是等比数列，并求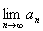。 解：（1）∵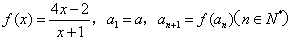
，
数列{an}是常数列，
∴
，
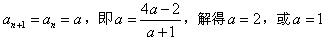∴所求实数a的值是1或2．
（2）∵
，
∴
，
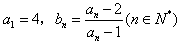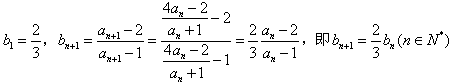∴数列{bn}是以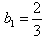
为首项，公比为
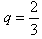的等比数列，
于是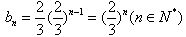
，
由
，
∴
。
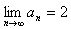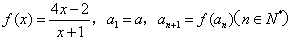，数列{an}是常数列，
∴
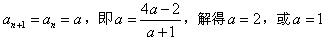，∴所求实数a的值是1或2．
（2）∵
，∴
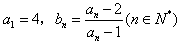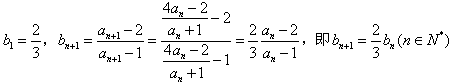，∴数列{bn}是以
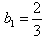为首项，公比为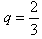的等比数列，于是
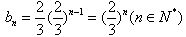，由
，∴
。
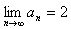练习册系列答案
相关题目
已知函数g(x)=
，函数f（x）=x2?g（x），则满足不等式f（a-2）+f（a2）＞0的实数a的取值范围是（ ）
|
| A、（-2，1） |
| B、（-1，2） |
| C、（-∞，-2）∪（1，+∞） |
| D、（-∞，-1）∪（2，+∞） |