题目内容
以双曲线
-
=1的右顶点为焦点的抛物线的标准方程为
| x2 |
| 16 |
| y2 |
| 9 |
y2=16x
y2=16x
.分析:根据双曲线方程,算出它的右顶点为(4,0),也是抛物线的焦点.由此设出抛物线方程为y2=2px,(p>0),结合抛物线焦点坐标的公式,可得p=8,从而得出该抛物线的标准方程.
解答:解析:∵双曲线的方程为
-
=1,
∴右顶点为(4,0).设抛物线的标准方程为y2=2px(p>0),
则
=4,即p=8,
∴抛物线的标准方程为y2=16x.故填y2=16x.
故答案为:y2=16x.
| x2 |
| 16 |
| y2 |
| 9 |
∴右顶点为(4,0).设抛物线的标准方程为y2=2px(p>0),
则
| p |
| 2 |
∴抛物线的标准方程为y2=16x.故填y2=16x.
故答案为:y2=16x.
点评:本题给出抛物线焦点与已知双曲线的右焦点重合,求抛物线的标准方程,着重考查了双曲线、抛物线的标准方程与简单几何性质等知识,属于基础题.

练习册系列答案
 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案
相关题目
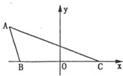 如图,△ABC外接圆半径R=
如图,△ABC外接圆半径R=14
| ||
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
下列双曲线中,以y=±
x为渐近线的是( )
| 1 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、x2-
|
 已知椭圆
已知椭圆