题目内容
9.在平面直角坐标系xOy中,曲线C1:x+y=4,曲线${C_2}:\left\{\begin{array}{l}x=1+cosθ\\ y=sinθ\end{array}\right.$(θ为参数),过原点O的直线l分别交C1,C2于A,B两点,则$\frac{{|{OB}|}}{{|{OA}|}}$的最大值为$\frac{{\sqrt{2}+1}}{4}$.分析 求出曲线${C_2}:\left\{\begin{array}{l}x=1+cosθ\\ y=sinθ\end{array}\right.$(θ为参数)的普通方程,设直线方程为kx-y=0,求出|OA|,|OB|,即可求出$\frac{{|{OB}|}}{{|{OA}|}}$的最大值.
解答 解:曲线${C_2}:\left\{\begin{array}{l}x=1+cosθ\\ y=sinθ\end{array}\right.$(θ为参数),普通方程为(x-1)2+y2=1.
设直线方程为kx-y=0,圆心到直线的距离d=$\frac{|k|}{\sqrt{{k}^{2}+1}}$,∴|OB|=2$\sqrt{1-\frac{{k}^{2}}{{k}^{2}+1}}$=$\frac{2}{\sqrt{{k}^{2}+1}}$,
kx-y=0与x+y=4联立,可得A($\frac{4}{k+1}$,$\frac{4k}{k+1}$),∴|OA|=$\sqrt{\frac{16(1+{k}^{2})}{(k+1)^{2}}}$,
∴$\frac{{|{OB}|}}{{|{OA}|}}$=$\frac{k+1}{2({k}^{2}+1)}$,
设k+1=t(t>0),则$\frac{{|{OB}|}}{{|{OA}|}}$=$\frac{1}{2t+\frac{4}{t}-4}$≤$\frac{1}{4\sqrt{2}-4}$=$\frac{{\sqrt{2}+1}}{4}$.
∴$\frac{{|{OB}|}}{{|{OA}|}}$的最大值为$\frac{{\sqrt{2}+1}}{4}$.
故答案为$\frac{{\sqrt{2}+1}}{4}$.
点评 本题考查参数方程与普通方程的转化,考查距离的计算,考查学生的计算能力,属于中档题.

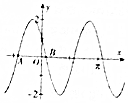 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的图象如图所示,其中A(-$\frac{5π}{12}$,0),B($\frac{π}{12}$,0),则函数f(x)的单调增区间为( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的图象如图所示,其中A(-$\frac{5π}{12}$,0),B($\frac{π}{12}$,0),则函数f(x)的单调增区间为( )| A. | [-$\frac{π}{6}$+kπ,$\frac{π}{3}$+kπ](k∈Z) | B. | [$\frac{π}{3}$+kπ,$\frac{5π}{6}$+kπ](k∈Z) | ||
| C. | [-$\frac{π}{6}$+2kπ,$\frac{π}{3}$+2kπ](k∈Z) | D. | [$\frac{π}{3}$+2kπ,$\frac{5π}{6}$+2kπ](k∈Z) |
| A. | 10-ln3 | B. | 8-ln3 | C. | $\frac{22}{3}$ | D. | $\frac{64}{9}$ |
| A. | $\frac{{y}^{2}}{2}-\frac{{x}^{2}}{3}$=1 | B. | y2-$\frac{{x}^{2}}{4}$=1 | C. | $\frac{{y}^{2}}{4}$-x2=1 | D. | $\frac{{y}^{2}}{3}-\frac{{x}^{2}}{2}$=1 |
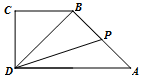 如图,在直角梯形ABCD中,AD∥BC,∠ADC=90°,AD=2,BC=CD=1,P是AB的中点,则$\overrightarrow{DP}•\overrightarrow{AB}$=-1.
如图,在直角梯形ABCD中,AD∥BC,∠ADC=90°,AD=2,BC=CD=1,P是AB的中点,则$\overrightarrow{DP}•\overrightarrow{AB}$=-1.