题目内容
【题目】已知向量 
， 
满足| |= 
，| |=1，且对任意实数x，不等式| +x |≥| + |恒成立，设 与 的夹角为θ，则tan2θ=（ ）
A.﹣ 
B.
C.﹣ 
D.
【答案】D
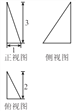
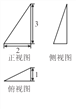
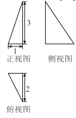
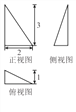
【解析】解：由平面向量加法的几何意义，只有当（ 
） 
时，对于任意实数x，不等式| 
+x 
|≥| + |恒成立，如图所示，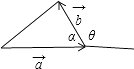 
设 
或 
，
斜边大于直角边恒成立，
则不等式| +x |≥| + |恒成立，
∵向量 ， 满足| |= 
，| |=1，
∴tanθ=﹣2，
∴tan2θ= 
．
故选：D．
另：将不等式| +x |≥| + |两边平方得到不等式| +x |2≥| + |2 ， 展开整理得得， 
恒成立，
所以判别式 
，解得cosθ= 
，sinθ= 
，所以tanθ=﹣2，tan2θ= 
；
故选D．
【考点精析】通过灵活运用数量积表示两个向量的夹角，掌握设
、
都是非零向量，
，
，
是与
的夹角，则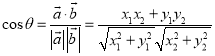
即可以解答此题．
练习册系列答案
相关题目
