题目内容
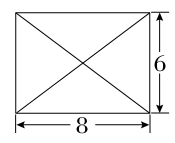
已知某几何体的俯视图是如图所示的矩形,正视图是一个底边长为8,高为4的等腰三角形,侧视图(或称左视图)是一个底边长为6,高为4的等腰三角形.
(1)求该几何体的体积V;
(2)求该几何体的侧面积S.
(1)求该几何体的体积V;
(2)求该几何体的侧面积S.

(1)64 (2)40+24

解:本题考查由三视图求几何体的侧面积和体积,由正视图和侧视图的三角形结合俯视图可知该几何体是一个底面为矩形,高为4,顶点在底面的射影是矩形中心的四棱锥,如图.

(1)V= ×(8×6)×4=64.
×(8×6)×4=64.
(2)四棱锥的两个侧面VAD、VBC是全等的等腰三角形,取BC的中点E,连接OE,VE,则△VOE为直角三角形,VE为△VBC边上的高,VE= =4
=4 .
.
同理侧面VAB、VCD也是全等的等腰三角形,
AB边上的高h= =5.
=5.
∴S侧=2×( ×6×4
×6×4 +
+ ×8×5)=40+24
×8×5)=40+24 .
.

(1)V=
 ×(8×6)×4=64.
×(8×6)×4=64.(2)四棱锥的两个侧面VAD、VBC是全等的等腰三角形,取BC的中点E,连接OE,VE,则△VOE为直角三角形,VE为△VBC边上的高,VE=
 =4
=4 .
.同理侧面VAB、VCD也是全等的等腰三角形,
AB边上的高h=
 =5.
=5.∴S侧=2×(
 ×6×4
×6×4 +
+ ×8×5)=40+24
×8×5)=40+24 .
.
练习册系列答案
相关题目
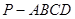 中,底面
中,底面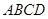 是边长为
是边长为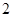 的正方形,侧棱
的正方形,侧棱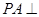 底面
底面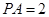 ,
,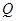 是
是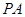 的中点.
的中点.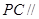 平面
平面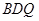 ;
;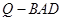 的体积.
的体积.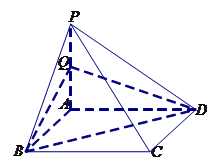
 中,底面ABCD和侧面
中,底面ABCD和侧面 都是矩形,E是CD的中点,
都是矩形,E是CD的中点,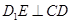 ,
, .
. ;
; ,求三棱锥
,求三棱锥 的体积.
的体积.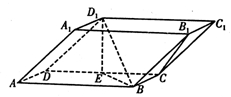
 的正三棱锥
的正三棱锥 中,
中, 长为
长为 ,
, 为棱
为棱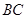 的中点,求
的中点,求
 与
与 所成角的大小(结果用反三角函数值表示);
所成角的大小(结果用反三角函数值表示);


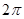

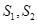 ,体积为
,体积为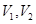 ,若它们的侧面积相等且
,若它们的侧面积相等且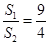 ,则
,则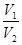 的值是 .
的值是 . 中,底面
中,底面 为边长为
为边长为 的正三角形,顶点
的正三角形,顶点 在底面
在底面 的中心, 若
的中心, 若 为
为 的中点,且直线
的中点,且直线 与底面
与底面 ,则三棱锥
,则三棱锥