题目内容
设正四棱锥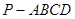 的侧面积为
的侧面积为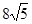 ,若
,若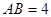 .
.

(1)求四棱锥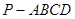 的体积;
的体积;
(2)求直线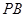 与平面
与平面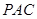 所成角的大小.
所成角的大小.
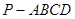 的侧面积为
的侧面积为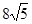 ,若
,若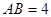 .
.
(1)求四棱锥
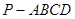 的体积;
的体积;(2)求直线
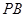 与平面
与平面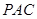 所成角的大小.
所成角的大小.(1)
(2))

(2))

试题分析:解(1)联结
 交
交 于
于 ,取
,取 的中点
的中点 ,联结
,联结 ,
, ,
, ,则
,则 ,
, ,
,  . 4分
. 4分所以四棱锥
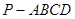 的体积
的体积 . 6分
. 6分(2)在正四棱锥
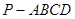 中,
中,
 平面
平面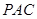 ,所以
,所以 就是直线
就是直线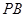 与平面
与平面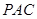 所成的角. 11分
所成的角. 11分在
 中,
中, ,所以直线
,所以直线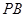 与平面
与平面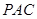 所成角的大小为
所成角的大小为 . 14分
. 14分点评:主要是考查了四棱锥体积的求解以及线面角的运用,属于基础题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
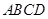 是正方形,
是正方形,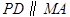 ,
,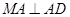 ,
, ,
, 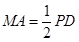 .
.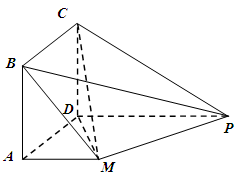
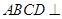 平面
平面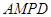 ;
;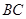 与
与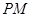 所成的角为
所成的角为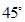 ,求二面角
,求二面角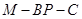 的余弦值.
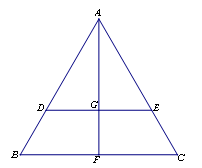
的余弦值.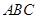 中,
中,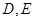 分别是
分别是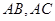 边上的点,
边上的点,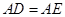 ,
,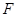 是
是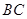 的中点,
的中点,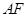 与
与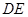 交于点
交于点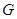 ,将
,将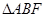 沿
沿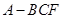 ,其中
,其中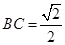 .
.
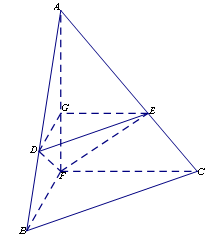
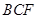 ;
;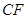
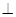 平面
平面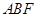 ;
;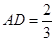 时,求三棱锥
时,求三棱锥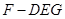 的体积
的体积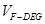 .
. 是边长为
是边长为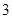 的
的 为正方形的对角线,将
为正方形的对角线,将 绕直线
绕直线 旋转一周后形成的几何体的体积等于 .
旋转一周后形成的几何体的体积等于 .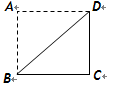
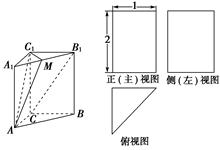
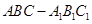 中,
中, 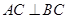 ,
, ,
,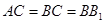 ,点
,点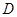 是
是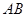 的中点,
的中点,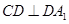 .
.
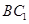 ∥平面
∥平面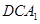 ;
;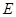 在线段
在线段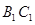 上,
上, ,且使直线
,且使直线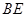 和平面
和平面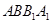 所成的角的正弦值为
所成的角的正弦值为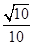 ,求
,求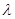 的值.
的值.  折成直角二面角,且
折成直角二面角,且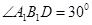 .
.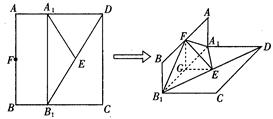
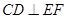
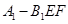 的体积.
的体积.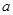 .
.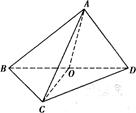
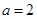 时,求证:AO⊥平面BCD;
时,求证:AO⊥平面BCD;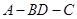 的大小为
的大小为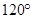 时,求二面角
时,求二面角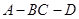 的正切值.
的正切值.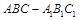 中,侧面
中,侧面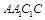 是边长为2的正方形,
是边长为2的正方形,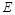 是
是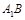 的中点,
的中点,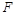 在棱
在棱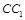 上.
上.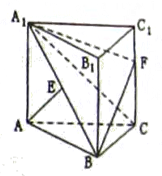
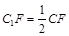 时,求三棱锥
时,求三棱锥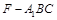 的体积.
的体积.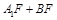 最小时,判断直线
最小时,判断直线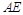 与
与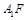 是否垂直,并证明结论.
是否垂直,并证明结论.