题目内容
已知数列an=1+| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
分析:先验证当n=1时成立,然后假设当n=k时成立来证明当n=k+1时成立.这里变换Sk+1=Sk+ak+1、ak=ak+1-
代入即可证明.
| 1 |
| k+1 |
解答:证明:当n=1时,a1=1
S1=a1=1满足条件
假设当n=k,(k>1,k∈N)时Sk=(k+1)ak-k成立
当n=k+1时,
∵ak=1+
+
+…+
=1+
+
+…+
+
-
=ak+1-
则Sk+1=Sk+ak+1=(k+1)ak-k+ak+1=(k+1)(ak+1-
)-k+ak+1
=(k+1)ak+1-1-k+ak+1=(k+2)ak+1-(1+k)
从而Sn=(n+1)an-n成立.
得证.
S1=a1=1满足条件
假设当n=k,(k>1,k∈N)时Sk=(k+1)ak-k成立
当n=k+1时,
∵ak=1+
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| k |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| k |
| 1 |
| k+1 |
| 1 |
| k+1 |
| 1 |
| k+1 |
则Sk+1=Sk+ak+1=(k+1)ak-k+ak+1=(k+1)(ak+1-
| 1 |
| k+1 |
=(k+1)ak+1-1-k+ak+1=(k+2)ak+1-(1+k)
从而Sn=(n+1)an-n成立.
得证.
点评:本题主要考查数列求出和数学归纳法.数学归纳法是一种证明题常用的方法,尤其是证明比较复杂的式子成立时,能够显现其优越性.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
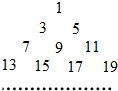 (2011•潍坊二模)已知数列an=2n-1(n∈N*),把数列{an}的各项排成如图所示的三角形数阵,记(m,n)表示该数阵中第m行中从左到右的第n个数,则S(10,6)对应于数阵中的数是
(2011•潍坊二模)已知数列an=2n-1(n∈N*),把数列{an}的各项排成如图所示的三角形数阵,记(m,n)表示该数阵中第m行中从左到右的第n个数,则S(10,6)对应于数阵中的数是