题目内容
(教材江苏版第62页习题7)(1)已知数列an的通项公式为an=| 1 |
| n(n+1) |
| 1 | ||||
|
分析:(1)an=
=
-
,可利用裂项求和的方法求解数列的和
(2)an=
=
-
,代入可求
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
(2)an=
| 1 | ||||
|
| ||||||||
(
|
| n+1 |
| n |
解答:解:(1)∵an=
=
-
∴Sn=a1+a2+…+an
=1-
+
-
+…+
-
=1-
=
an=
=
=
-
Tn=a1+a2+…+an
=
-1+
-
+…+
-
=
-1
故答案为:
;
-1
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
∴Sn=a1+a2+…+an
=1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| 1+n |
=
| n |
| 1+n |
an=
| 1 | ||||
|
=
| ||||||||
(
|
| n+1 |
| n |
Tn=a1+a2+…+an
=
| 2 |
| 3 |
| 2 |
| n+1 |
| n |
| n+1 |
故答案为:
| n |
| n+1 |
| n+1 |
点评:本题主要考查了数列求和的常见的方法:裂项求和.属于对基础知识及基本方法的考查,考查考生的基本运算的能力.

练习册系列答案
相关题目
 ,则前n项的和 ________;(2)已知数列an的通项公式为
,则前n项的和 ________;(2)已知数列an的通项公式为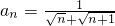 ,则前n项的和 ________.
,则前n项的和 ________. ,则前n项的和 ;(2)已知数列an的通项公式为
,则前n项的和 ;(2)已知数列an的通项公式为 ,则前n项的和 .
,则前n项的和 .