题目内容
若θ是钝角,则满足等式log2(x2-x+3)=sinθ-| 3 |
分析:由log2(x2-x+3)=sinθ-
cosθ=2sin(θ-
)结合已知
<θ<π可求2sin(θ-
)的范围,进而可得log2(x2-x+3)的取值范围,解对数不等式可得x的范围
| 3 |
| π |
| 3 |
| π |
| 2 |
| π |
| 3 |
解答:解:∵log2(x2-x+3)=sinθ-
cosθ=2sin(θ-
)
∵
<θ<π
∴
<θ-
<
∴
<sin(θ-
)≤1
从而有1<log2(x2-x+3)≤2
∴2<x2-x+3≤4
解不等式可得
≤ x ≤
故答案为:[
,
]
| 3 |
| π |
| 3 |
∵
| π |
| 2 |
∴
| π |
| 6 |
| π |
| 3 |
| 2π |
| 3 |
∴
| 1 |
| 2 |
| π |
| 3 |
从而有1<log2(x2-x+3)≤2
∴2<x2-x+3≤4
解不等式可得
1-
| ||
| 2 |
1+
| ||
| 2 |
故答案为:[
1-
| ||
| 2 |
1+
| ||
| 2 |
点评:本题综合考查了辅助角公式,正弦函数的值域的求解,对数不等式的解法,是一道综合性比较好的试题.

练习册系列答案
相关题目
若O是△ABC所在平面内的一点,且向量
,
,
满足条件
+
=-
,|
|=|
|=|
|,则△ABC的形状是( )
| OA |
| OB |
| OC |
| OA |
| OB |
| OC |
| OA |
| OB |
| OC |
| A、钝角三角形 |
| B、锐角三角形 |
| C、直角三角形 |
| D、等边三角形 |
 内有一点
内有一点 ,满足
,满足 ,且
,且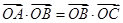 ,则
,则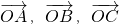 满足条件
满足条件 ,
, ,则△ABC的形状是
,则△ABC的形状是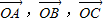 满足条件
满足条件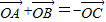 ,
,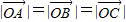 ,则△ABC的形状是( )
,则△ABC的形状是( )